Causal Machine Learning in StochTree
Causal-Inference.RmdThis vignette demonstrates how to use the bcf() function
for supervised learning. To begin, we load the stochtree package.
We also define several simple functions that configue the data generating processes used in this vignette.
g <- function(x) {ifelse(x[,5]==1,2,ifelse(x[,5]==2,-1,-4))}
mu1 <- function(x) {1+g(x)+x[,1]*x[,3]}
mu2 <- function(x) {1+g(x)+6*abs(x[,3]-1)}
tau1 <- function(x) {rep(3,nrow(x))}
tau2 <- function(x) {1+2*x[,2]*x[,4]}Demo 1: Nonlinear Outcome Model, Heterogeneous Treatment Effect
We consider the following data generating process from Hahn, Murray, and Carvalho (2020):
\[\begin{equation*} \begin{aligned} y &= \mu(X) + \tau(X) Z + \epsilon\\ \epsilon &\sim N\left(0,\sigma^2\right)\\ \mu(X) &= 1 + g(X) + 6 \lvert X_3 - 1 \rvert\\ \tau(X) &= 1 + 2 X_2 X_4\\ g(X) &= \mathbb{I}(X_5=1) \times 2 - \mathbb{I}(X_5=2) \times 1 - \mathbb{I}(X_5=3) \times 4\\ X_1,X_2,X_3 &\sim N\left(0,1\right)\\ X_4 &\sim \text{Bernoulli}(1/2)\\ X_5 &\sim \text{Categorical}(1/3,1/3,1/3)\\ \end{aligned} \end{equation*}\]
Simulation
We draw from the DGP defined above
n <- 500
snr <- 3
x1 <- rnorm(n)
x2 <- rnorm(n)
x3 <- rnorm(n)
x4 <- as.numeric(rbinom(n,1,0.5))
x5 <- as.numeric(sample(1:3,n,replace=T))
X <- cbind(x1,x2,x3,x4,x5)
p <- ncol(X)
mu_x <- mu1(X)
tau_x <- tau2(X)
pi_x <- 0.8*pnorm((3*mu_x/sd(mu_x)) - 0.5*X[,1]) + 0.05 + runif(n)/10
Z <- rbinom(n,1,pi_x)
E_XZ <- mu_x + Z*tau_x
y <- E_XZ + rnorm(n, 0, 1)*(sd(E_XZ)/snr)
# Split data into test and train sets
test_set_pct <- 0.2
n_test <- round(test_set_pct*n)
n_train <- n - n_test
test_inds <- sort(sample(1:n, n_test, replace = F))
train_inds <- (1:n)[!((1:n) %in% test_inds)]
X_test <- X[test_inds,]
X_train <- X[train_inds,]
pi_test <- pi_x[test_inds]
pi_train <- pi_x[train_inds]
Z_test <- Z[test_inds]
Z_train <- Z[train_inds]
y_test <- y[test_inds]
y_train <- y[train_inds]
mu_test <- mu_x[test_inds]
mu_train <- mu_x[train_inds]
tau_test <- tau_x[test_inds]
tau_train <- tau_x[train_inds]Sampling and Analysis
Warmstart
We first simulate from an ensemble model of \(y \mid X\) using “warm-start”
initialization samples (Krantsevich, He, and Hahn
(2023)). This is the default in stochtree.
num_gfr <- 10
num_burnin <- 0
num_mcmc <- 1000
num_samples <- num_gfr + num_burnin + num_mcmc
bcf_model_warmstart <- bcf(
X_train = X_train, Z_train = Z_train, y_train = y_train, pi_train = pi_train,
X_test = X_test, Z_test = Z_test, pi_test = pi_test, feature_types = c(0,0,0,1,1),
num_gfr = num_gfr, num_burnin = num_burnin, num_mcmc = num_mcmc,
sample_sigma_leaf_mu = F, sample_sigma_leaf_tau = F
)Inspect the BART samples that were initialized with an XBART warm-start
sample_inds <- (num_gfr+1):num_samples
plot(rowMeans(bcf_model_warmstart$mu_hat_test[,sample_inds]), mu_test,
xlab = "predicted", ylab = "actual", main = "Prognostic function")
abline(0,1,col="red",lty=3,lwd=3)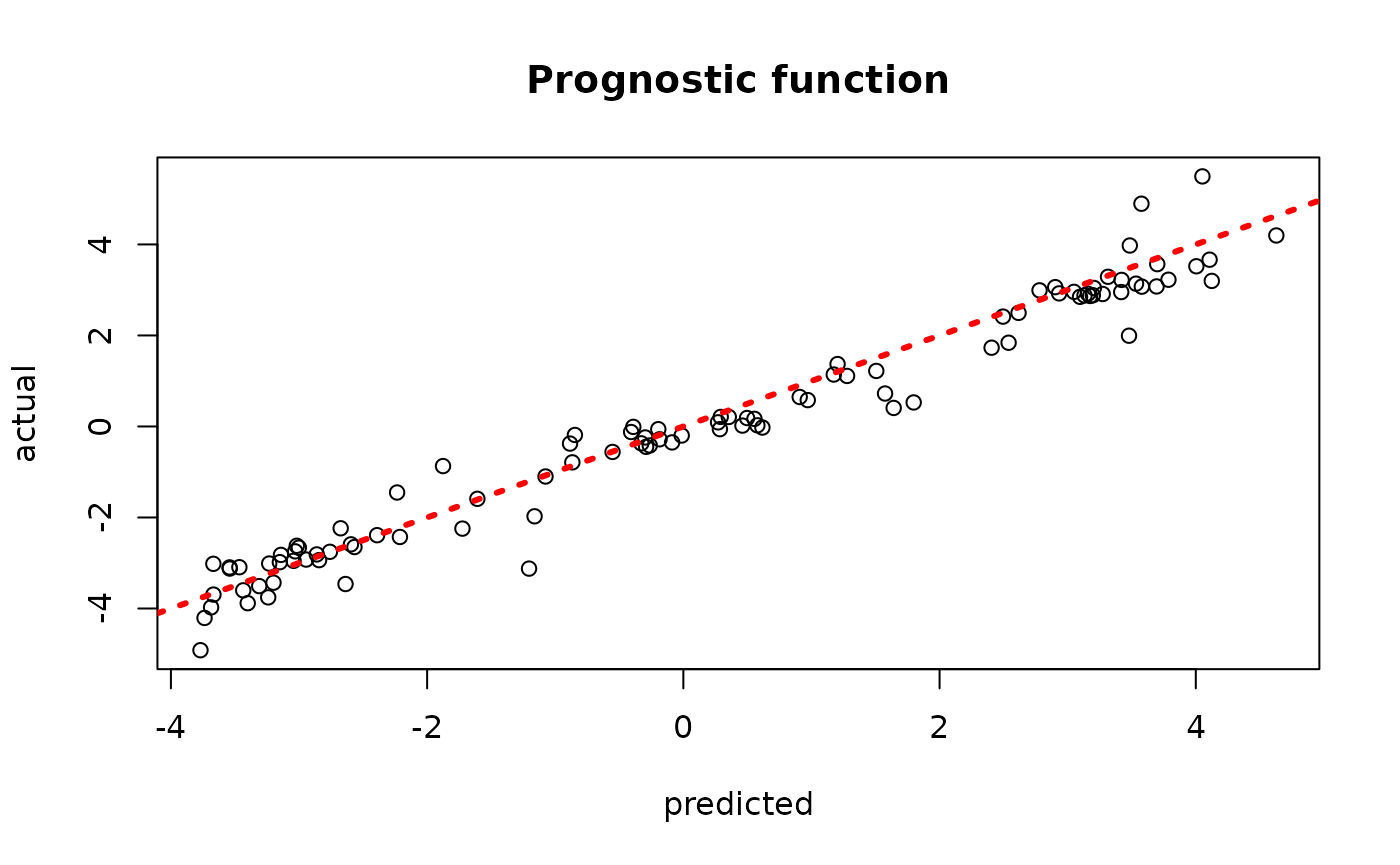
plot(rowMeans(bcf_model_warmstart$tau_hat_test[,sample_inds]), tau_test,
xlab = "predicted", ylab = "actual", main = "Treatment effect")
abline(0,1,col="red",lty=3,lwd=3)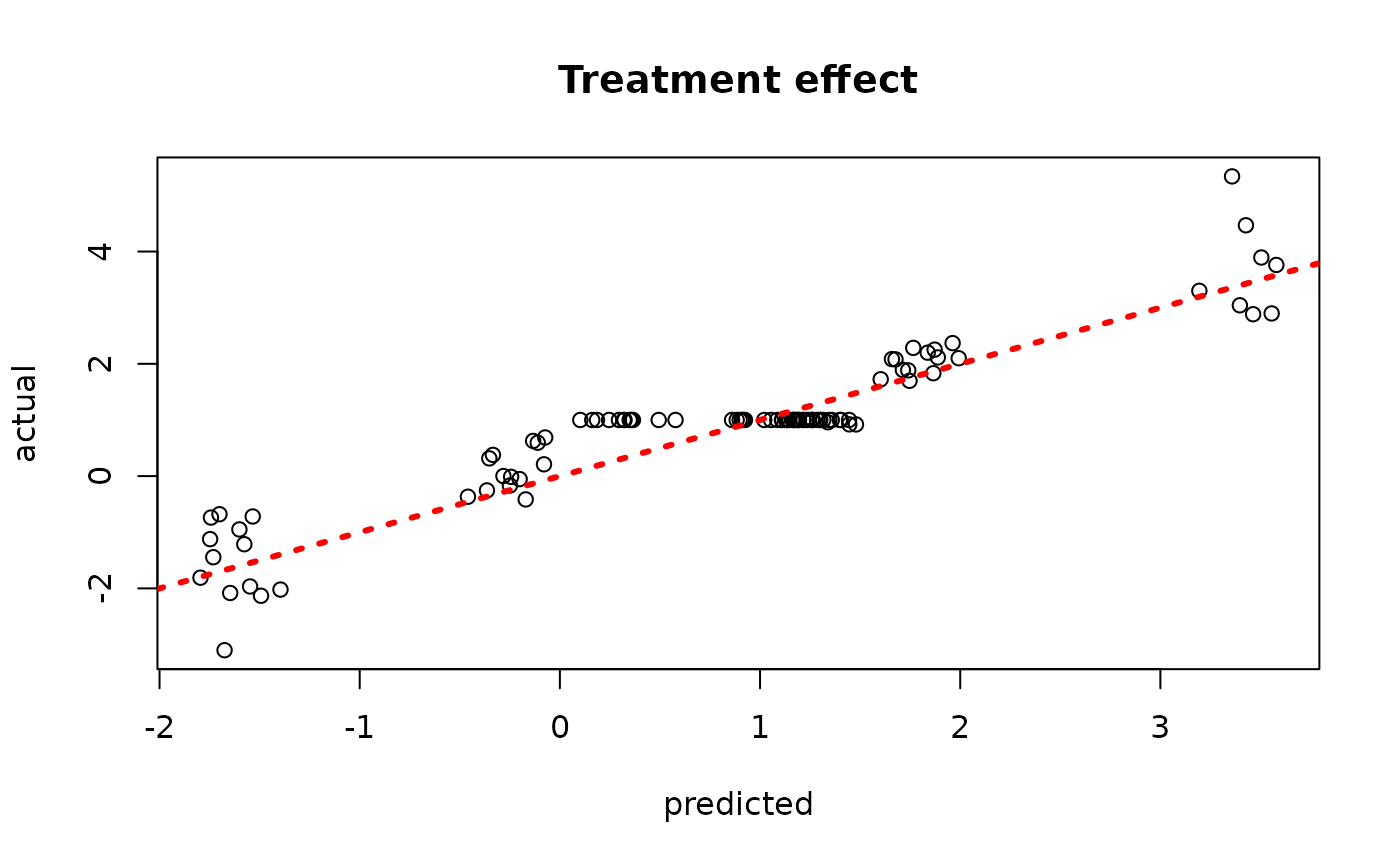
sigma_observed <- var(y-E_XZ)
plot_bounds <- c(min(c(bcf_model_warmstart$sigma2_samples[sample_inds], sigma_observed)),
max(c(bcf_model_warmstart$sigma2_samples[sample_inds], sigma_observed)))
plot(bcf_model_warmstart$sigma2_samples[sample_inds], ylim = plot_bounds,
ylab = "sigma^2", xlab = "Sample", main = "Global variance parameter")
abline(h = sigma_observed, lty=3, lwd = 3, col = "blue")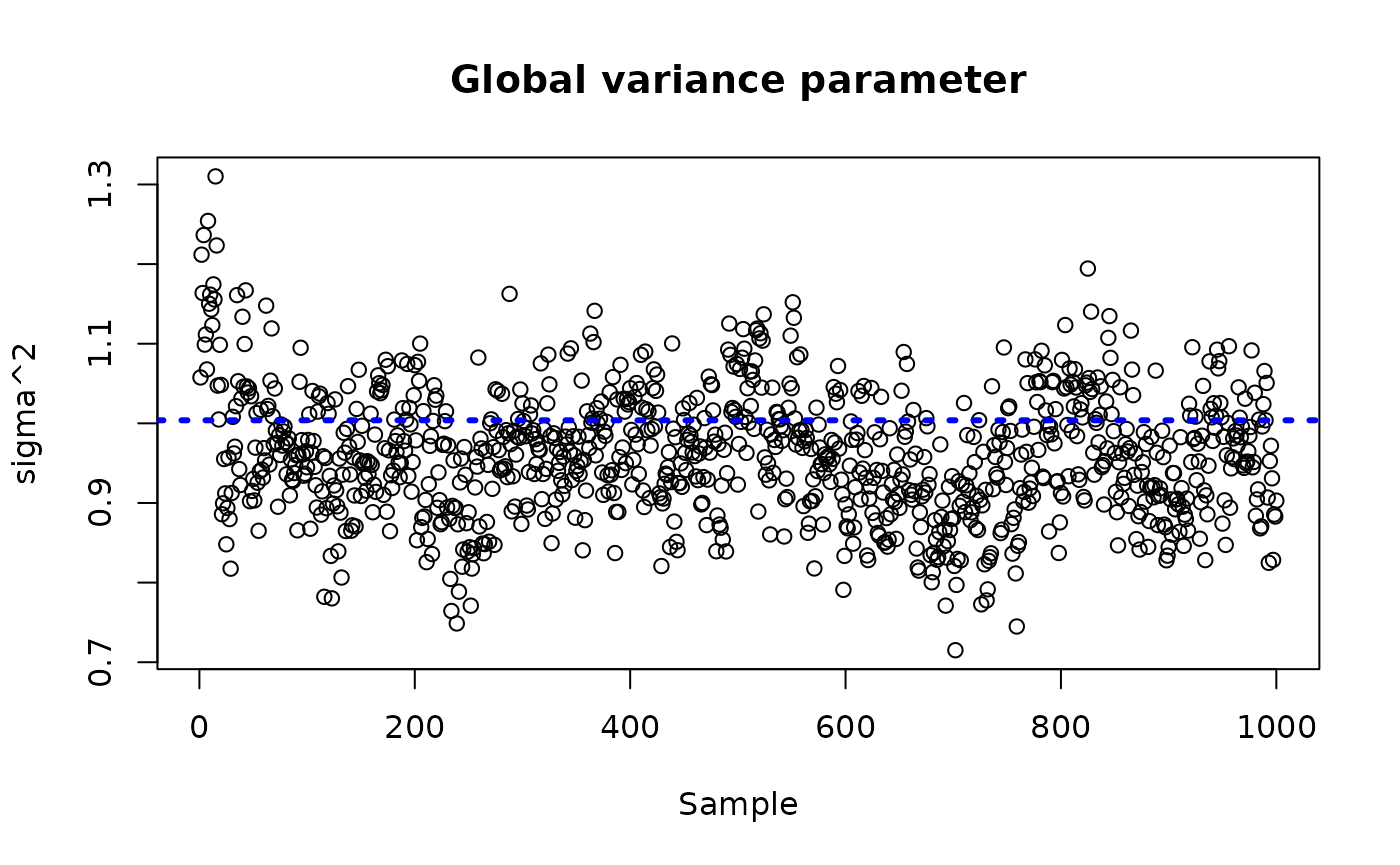
Examine test set interval coverage
BART MCMC without Warmstart
Next, we simulate from this ensemble model without any warm-start initialization.
num_gfr <- 0
num_burnin <- 1000
num_mcmc <- 1000
num_samples <- num_gfr + num_burnin + num_mcmc
bcf_model_root <- bcf(
X_train = X_train, Z_train = Z_train, y_train = y_train, pi_train = pi_train,
X_test = X_test, Z_test = Z_test, pi_test = pi_test, feature_types = c(0,0,0,1,1),
num_gfr = num_gfr, num_burnin = num_burnin, num_mcmc = num_mcmc,
sample_sigma_leaf_mu = F, sample_sigma_leaf_tau = F
)Inspect the BART samples after burnin
sample_inds <- (num_burnin+1):num_samples
plot(rowMeans(bcf_model_root$mu_hat_test[,sample_inds]), mu_test,
xlab = "predicted", ylab = "actual", main = "Prognostic function")
abline(0,1,col="red",lty=3,lwd=3)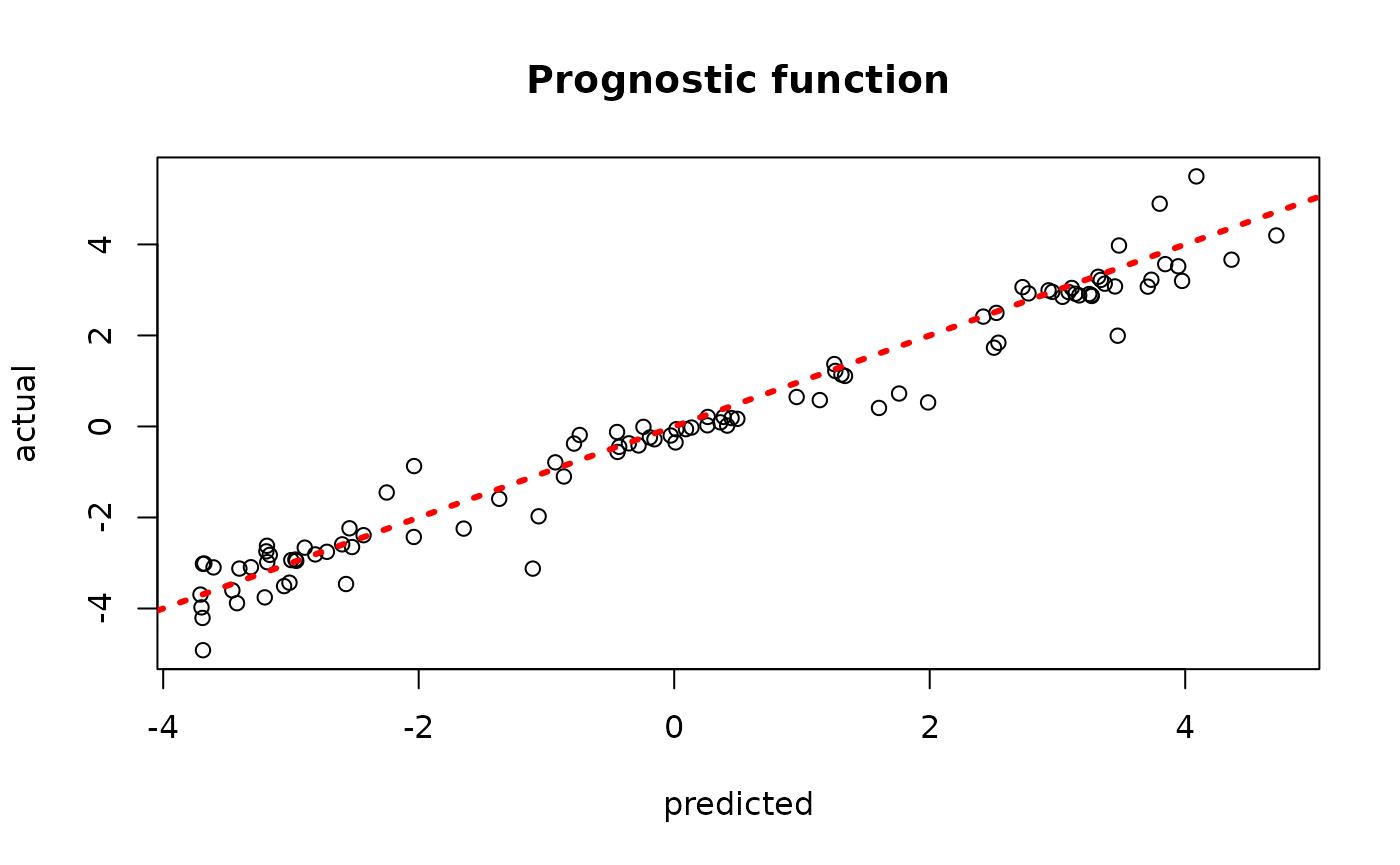
plot(rowMeans(bcf_model_root$tau_hat_test[,sample_inds]), tau_test,
xlab = "predicted", ylab = "actual", main = "Treatment effect")
abline(0,1,col="red",lty=3,lwd=3)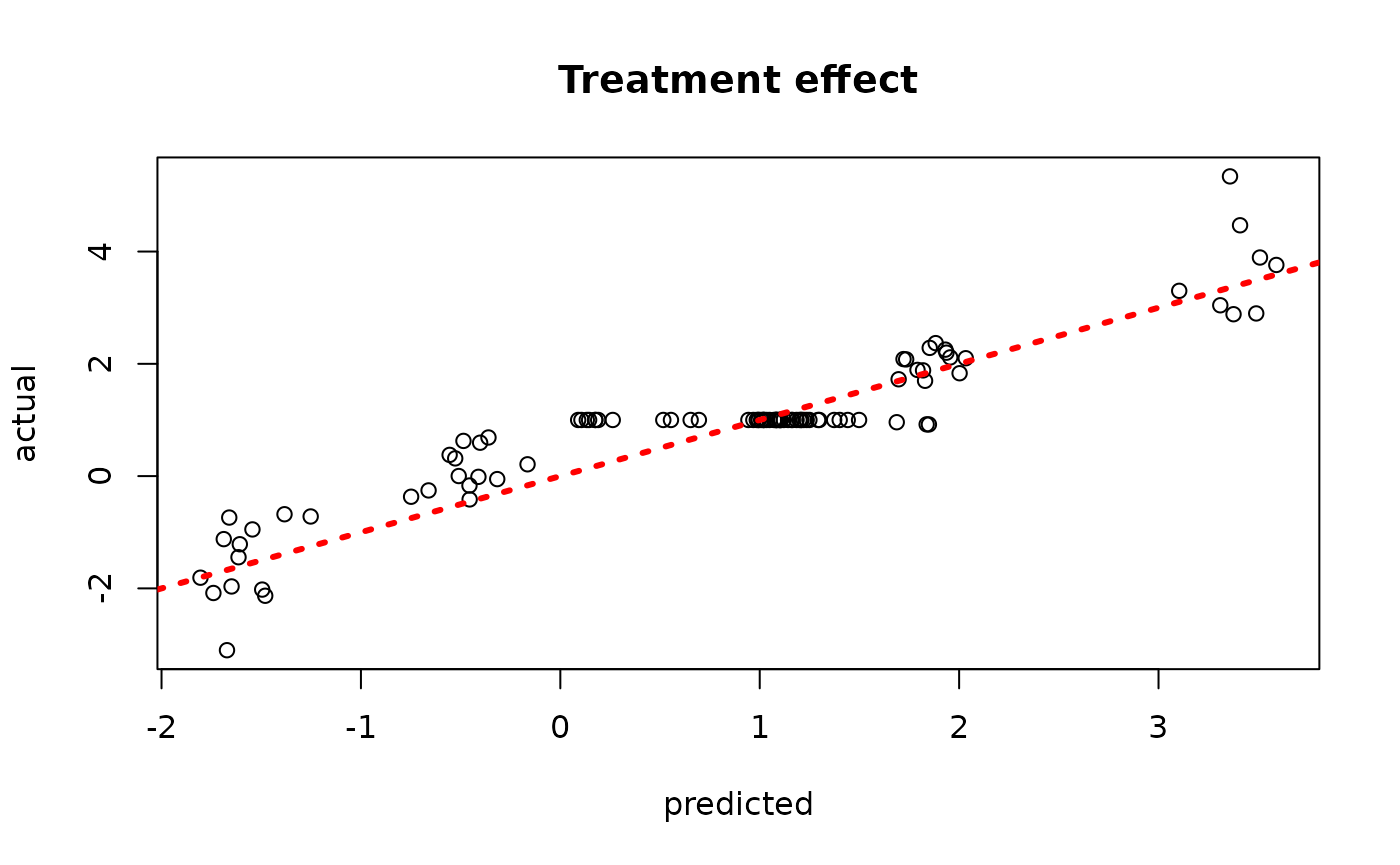
sigma_observed <- var(y-E_XZ)
plot_bounds <- c(min(c(bcf_model_root$sigma2_samples[sample_inds], sigma_observed)),
max(c(bcf_model_root$sigma2_samples[sample_inds], sigma_observed)))
plot(bcf_model_root$sigma2_samples[sample_inds], ylim = plot_bounds,
ylab = "sigma^2", xlab = "Sample", main = "Global variance parameter")
abline(h = sigma_observed, lty=3, lwd = 3, col = "blue")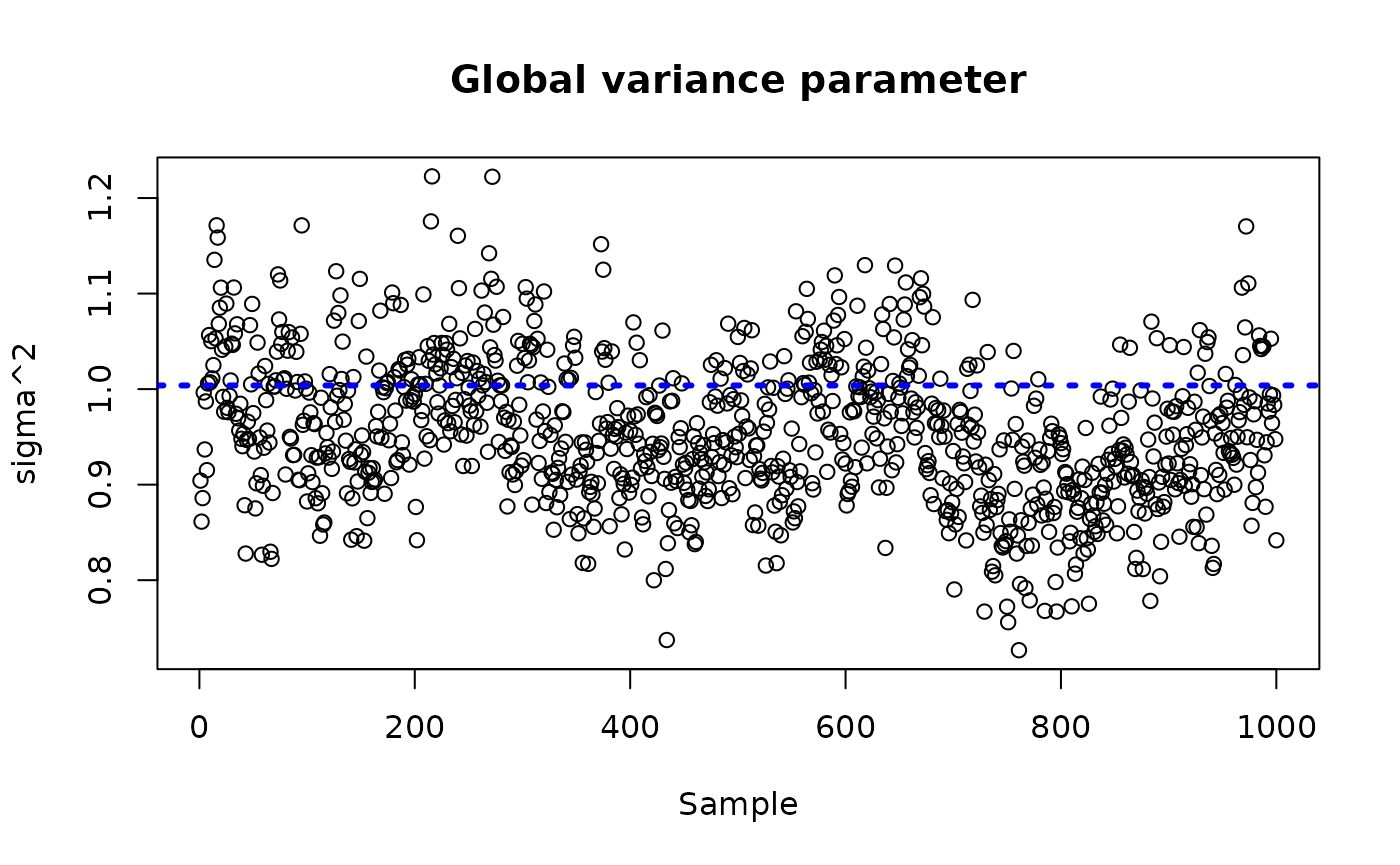
Examine test set interval coverage
Demo 2: Linear Outcome Model, Heterogeneous Treatment Effect
We consider the following data generating process from Hahn, Murray, and Carvalho (2020):
\[\begin{equation*} \begin{aligned} y &= \mu(X) + \tau(X) Z + \epsilon\\ \epsilon &\sim N\left(0,\sigma^2\right)\\ \mu(X) &= 1 + g(X) + 6 X_1 X_3\\ \tau(X) &= 1 + 2 X_2 X_4\\ g(X) &= \mathbb{I}(X_5=1) \times 2 - \mathbb{I}(X_5=2) \times 1 - \mathbb{I}(X_5=3) \times 4\\ X_1,X_2,X_3 &\sim N\left(0,1\right)\\ X_4 &\sim \text{Bernoulli}(1/2)\\ X_5 &\sim \text{Categorical}(1/3,1/3,1/3)\\ \end{aligned} \end{equation*}\]
Simulation
We draw from the DGP defined above
n <- 500
snr <- 3
x1 <- rnorm(n)
x2 <- rnorm(n)
x3 <- rnorm(n)
x4 <- as.numeric(rbinom(n,1,0.5))
x5 <- as.numeric(sample(1:3,n,replace=T))
X <- cbind(x1,x2,x3,x4,x5)
p <- ncol(X)
mu_x <- mu2(X)
tau_x <- tau2(X)
pi_x <- 0.8*pnorm((3*mu_x/sd(mu_x)) - 0.5*X[,1]) + 0.05 + runif(n)/10
Z <- rbinom(n,1,pi_x)
E_XZ <- mu_x + Z*tau_x
y <- E_XZ + rnorm(n, 0, 1)*(sd(E_XZ)/snr)
# Split data into test and train sets
test_set_pct <- 0.2
n_test <- round(test_set_pct*n)
n_train <- n - n_test
test_inds <- sort(sample(1:n, n_test, replace = F))
train_inds <- (1:n)[!((1:n) %in% test_inds)]
X_test <- X[test_inds,]
X_train <- X[train_inds,]
pi_test <- pi_x[test_inds]
pi_train <- pi_x[train_inds]
Z_test <- Z[test_inds]
Z_train <- Z[train_inds]
y_test <- y[test_inds]
y_train <- y[train_inds]
mu_test <- mu_x[test_inds]
mu_train <- mu_x[train_inds]
tau_test <- tau_x[test_inds]
tau_train <- tau_x[train_inds]Sampling and Analysis
Warmstart
We first simulate from an ensemble model of \(y \mid X\) using “warm-start”
initialization samples (Krantsevich, He, and Hahn
(2023)). This is the default in stochtree.
num_gfr <- 10
num_burnin <- 0
num_mcmc <- 100
num_samples <- num_gfr + num_burnin + num_mcmc
bcf_model_warmstart <- bcf(
X_train = X_train, Z_train = Z_train, y_train = y_train, pi_train = pi_train,
X_test = X_test, Z_test = Z_test, pi_test = pi_test, feature_types = c(0,0,0,1,1),
num_gfr = num_gfr, num_burnin = num_burnin, num_mcmc = num_mcmc,
sample_sigma_leaf_mu = F, sample_sigma_leaf_tau = F
)Inspect the BART samples that were initialized with an XBART warm-start
sample_inds <- (num_gfr+1):num_samples
plot(rowMeans(bcf_model_warmstart$mu_hat_test[,sample_inds]), mu_test,
xlab = "predicted", ylab = "actual", main = "Prognostic function")
abline(0,1,col="red",lty=3,lwd=3)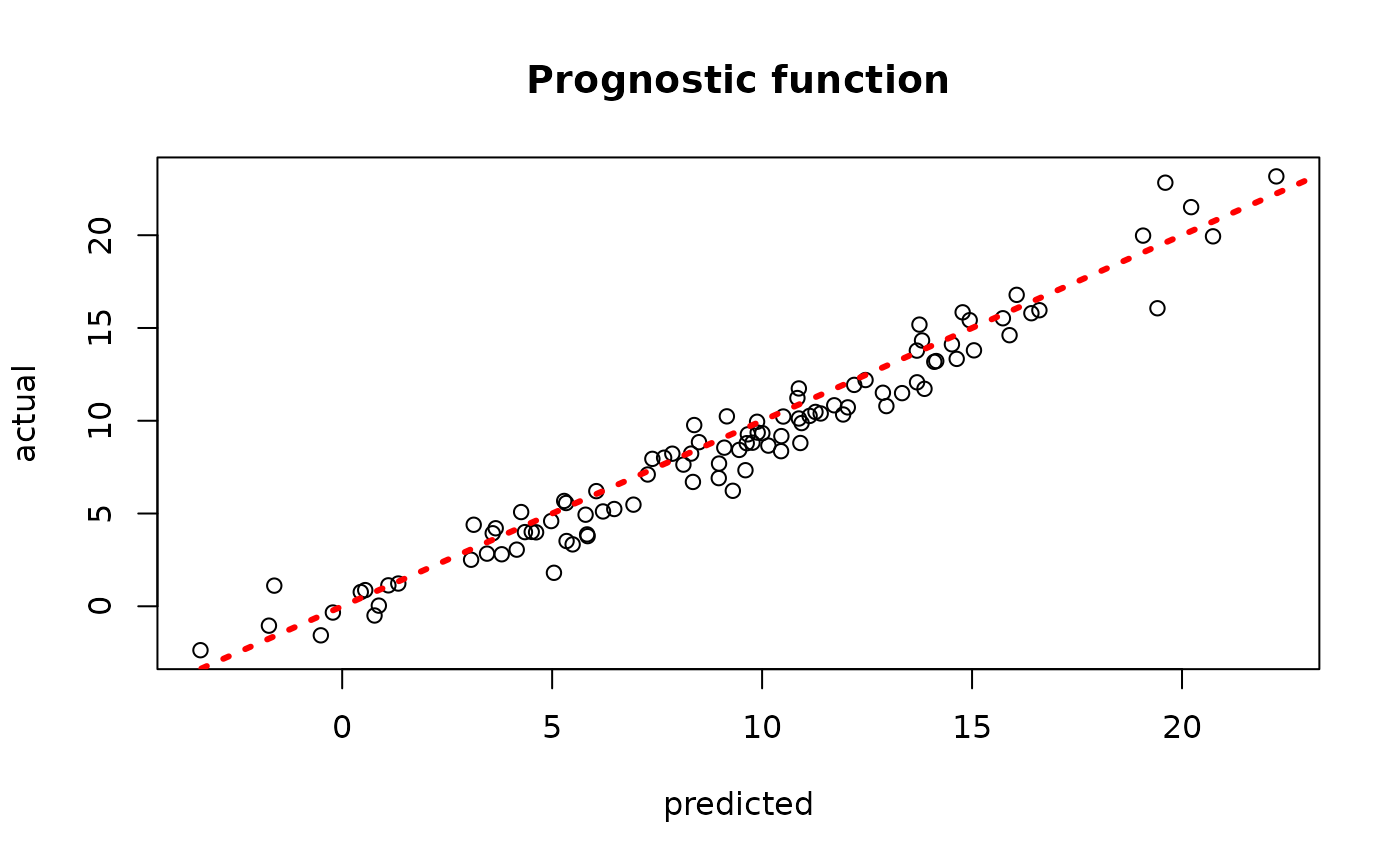
plot(rowMeans(bcf_model_warmstart$tau_hat_test[,sample_inds]), tau_test,
xlab = "predicted", ylab = "actual", main = "Treatment effect")
abline(0,1,col="red",lty=3,lwd=3)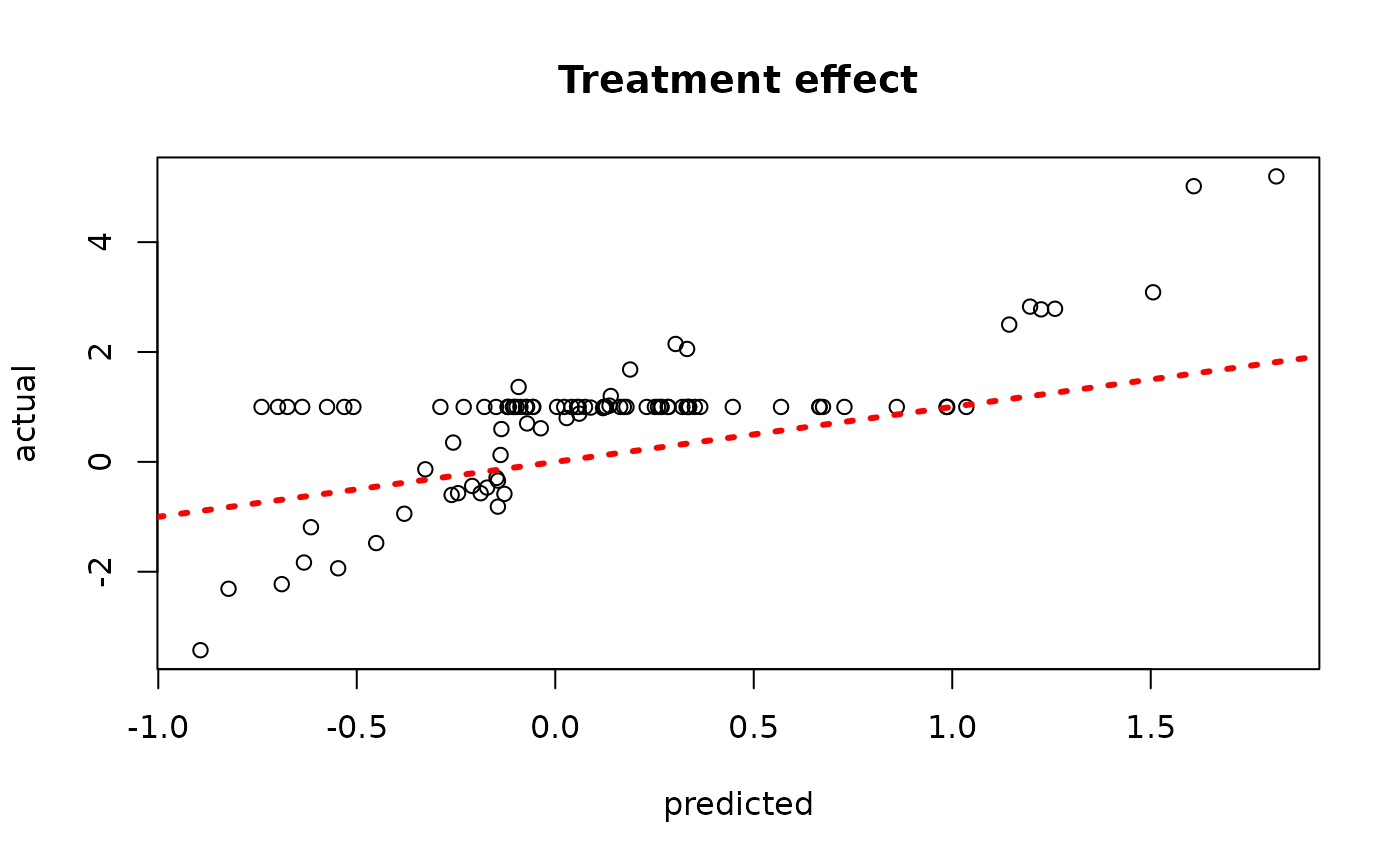
sigma_observed <- var(y-E_XZ)
plot_bounds <- c(min(c(bcf_model_warmstart$sigma2_samples[sample_inds], sigma_observed)),
max(c(bcf_model_warmstart$sigma2_samples[sample_inds], sigma_observed)))
plot(bcf_model_warmstart$sigma2_samples[sample_inds], ylim = plot_bounds,
ylab = "sigma^2", xlab = "Sample", main = "Global variance parameter")
abline(h = sigma_observed, lty=3, lwd = 3, col = "blue")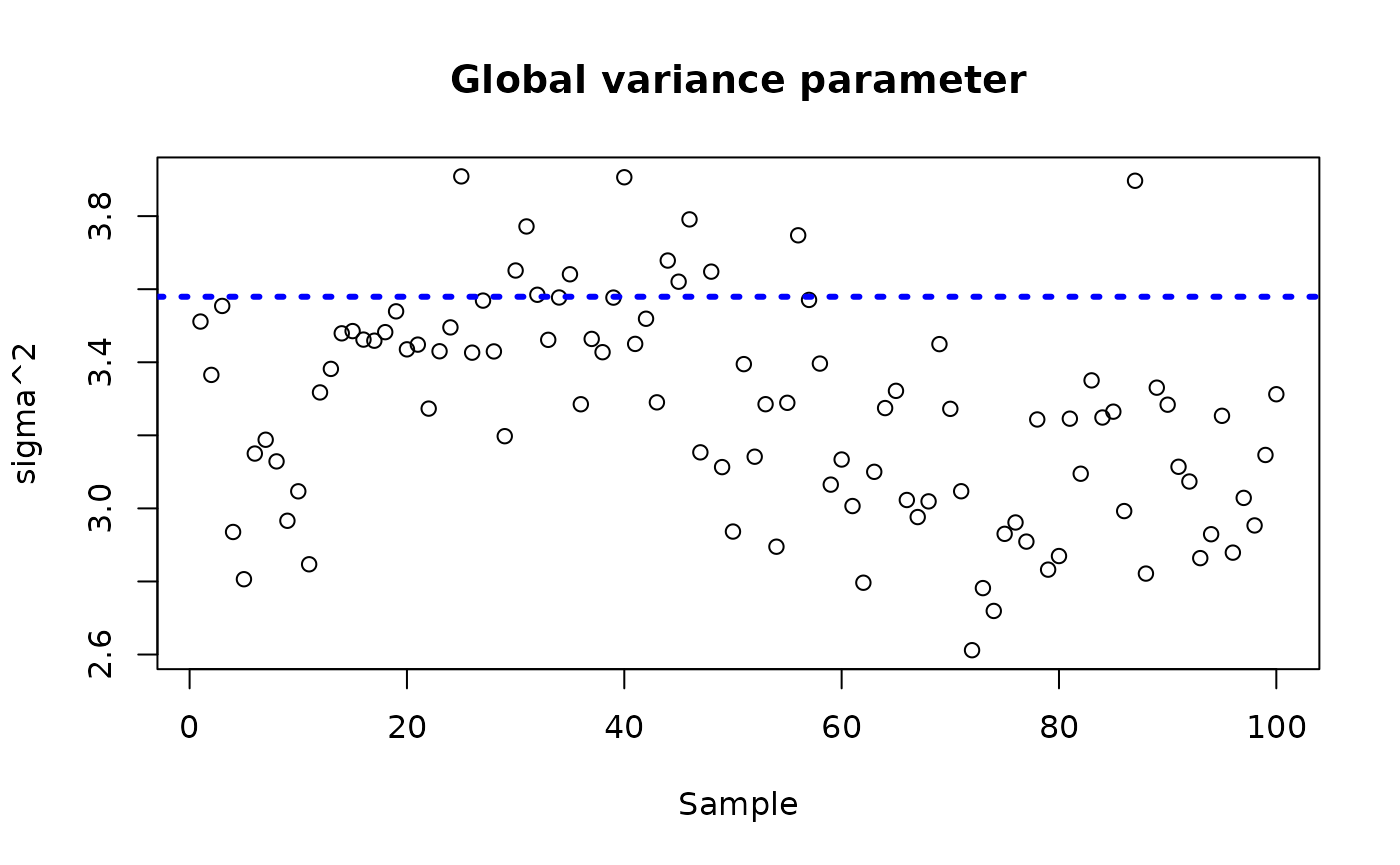
Examine test set interval coverage
BART MCMC without Warmstart
Next, we simulate from this ensemble model without any warm-start initialization.
num_gfr <- 0
num_burnin <- 100
num_mcmc <- 100
num_samples <- num_gfr + num_burnin + num_mcmc
bcf_model_root <- bcf(
X_train = X_train, Z_train = Z_train, y_train = y_train, pi_train = pi_train,
X_test = X_test, Z_test = Z_test, pi_test = pi_test, feature_types = c(0,0,0,1,1),
num_gfr = num_gfr, num_burnin = num_burnin, num_mcmc = num_mcmc,
sample_sigma_leaf_mu = F, sample_sigma_leaf_tau = F
)Inspect the BART samples after burnin
sample_inds <- (num_burnin+1):num_samples
plot(rowMeans(bcf_model_root$mu_hat_test[,sample_inds]), mu_test,
xlab = "predicted", ylab = "actual", main = "Prognostic function")
abline(0,1,col="red",lty=3,lwd=3)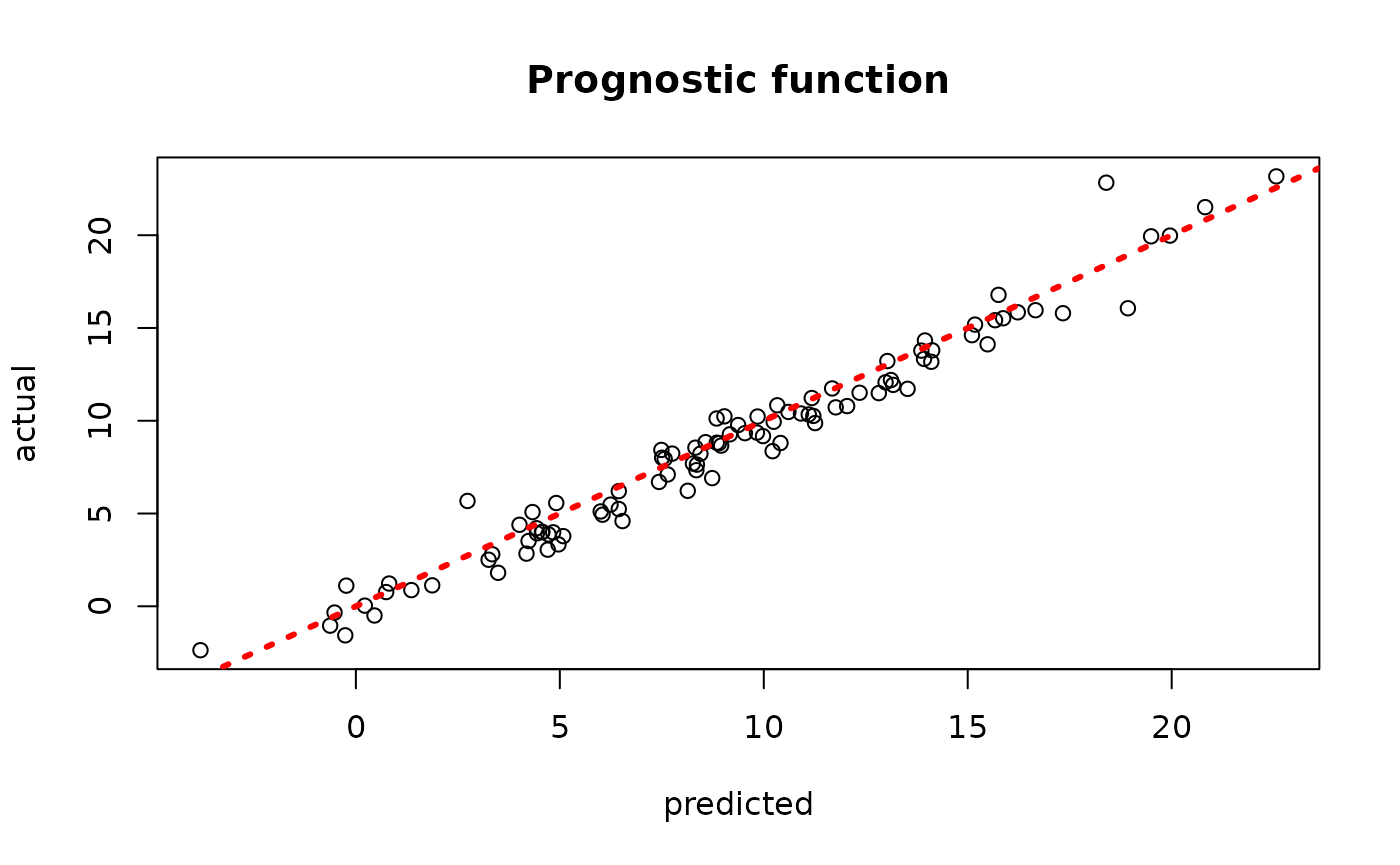
plot(rowMeans(bcf_model_root$tau_hat_test[,sample_inds]), tau_test,
xlab = "predicted", ylab = "actual", main = "Treatment effect")
abline(0,1,col="red",lty=3,lwd=3)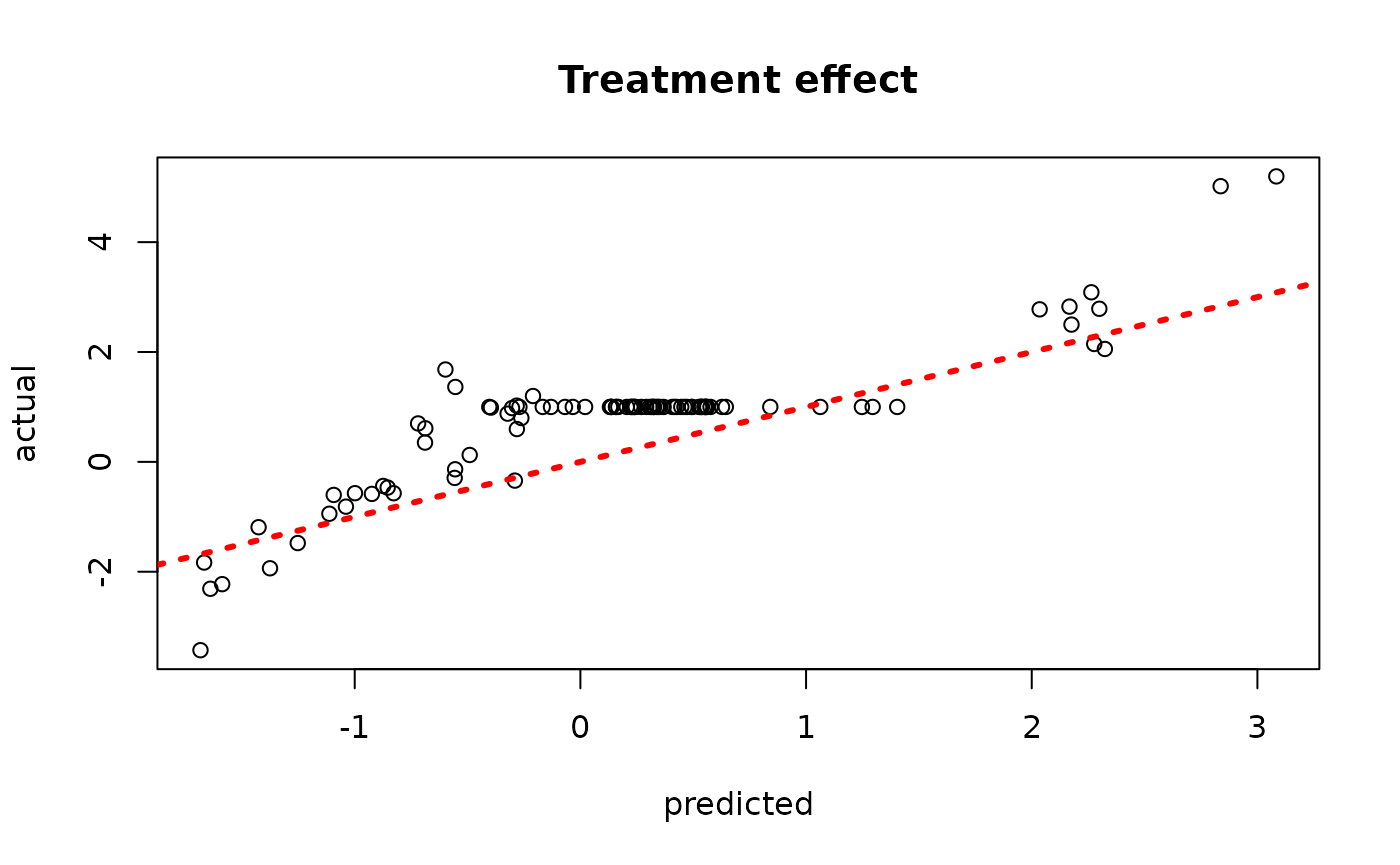
sigma_observed <- var(y-E_XZ)
plot_bounds <- c(min(c(bcf_model_root$sigma2_samples[sample_inds], sigma_observed)),
max(c(bcf_model_root$sigma2_samples[sample_inds], sigma_observed)))
plot(bcf_model_root$sigma2_samples[sample_inds], ylim = plot_bounds,
ylab = "sigma^2", xlab = "Sample", main = "Global variance parameter")
abline(h = sigma_observed, lty=3, lwd = 3, col = "blue")
Examine test set interval coverage
Demo 3: Linear Outcome Model, Homogeneous Treatment Effect
We consider the following data generating process from Hahn, Murray, and Carvalho (2020):
\[\begin{equation*} \begin{aligned} y &= \mu(X) + \tau(X) Z + \epsilon\\ \epsilon &\sim N\left(0,\sigma^2\right)\\ \mu(X) &= 1 + g(X) + 6 X_1 X_3\\ \tau(X) &= 3\\ g(X) &= \mathbb{I}(X_5=1) \times 2 - \mathbb{I}(X_5=2) \times 1 - \mathbb{I}(X_5=3) \times 4\\ X_1,X_2,X_3 &\sim N\left(0,1\right)\\ X_4 &\sim \text{Bernoulli}(1/2)\\ X_5 &\sim \text{Categorical}(1/3,1/3,1/3)\\ \end{aligned} \end{equation*}\]
Simulation
We draw from the DGP defined above
n <- 500
snr <- 3
x1 <- rnorm(n)
x2 <- rnorm(n)
x3 <- rnorm(n)
x4 <- as.numeric(rbinom(n,1,0.5))
x5 <- as.numeric(sample(1:3,n,replace=T))
X <- cbind(x1,x2,x3,x4,x5)
p <- ncol(X)
mu_x <- mu2(X)
tau_x <- tau1(X)
pi_x <- 0.8*pnorm((3*mu_x/sd(mu_x)) - 0.5*X[,1]) + 0.05 + runif(n)/10
Z <- rbinom(n,1,pi_x)
E_XZ <- mu_x + Z*tau_x
y <- E_XZ + rnorm(n, 0, 1)*(sd(E_XZ)/snr)
# Split data into test and train sets
test_set_pct <- 0.2
n_test <- round(test_set_pct*n)
n_train <- n - n_test
test_inds <- sort(sample(1:n, n_test, replace = F))
train_inds <- (1:n)[!((1:n) %in% test_inds)]
X_test <- X[test_inds,]
X_train <- X[train_inds,]
pi_test <- pi_x[test_inds]
pi_train <- pi_x[train_inds]
Z_test <- Z[test_inds]
Z_train <- Z[train_inds]
y_test <- y[test_inds]
y_train <- y[train_inds]
mu_test <- mu_x[test_inds]
mu_train <- mu_x[train_inds]
tau_test <- tau_x[test_inds]
tau_train <- tau_x[train_inds]Sampling and Analysis
Warmstart
We first simulate from an ensemble model of \(y \mid X\) using “warm-start”
initialization samples (Krantsevich, He, and Hahn
(2023)). This is the default in stochtree.
num_gfr <- 10
num_burnin <- 0
num_mcmc <- 100
num_samples <- num_gfr + num_burnin + num_mcmc
bcf_model_warmstart <- bcf(
X_train = X_train, Z_train = Z_train, y_train = y_train, pi_train = pi_train,
X_test = X_test, Z_test = Z_test, pi_test = pi_test, feature_types = c(0,0,0,1,1),
num_gfr = num_gfr, num_burnin = num_burnin, num_mcmc = num_mcmc,
sample_sigma_leaf_mu = F, sample_sigma_leaf_tau = F
)Inspect the BART samples that were initialized with an XBART warm-start
sample_inds <- (num_gfr+1):num_samples
plot(rowMeans(bcf_model_warmstart$mu_hat_test[,sample_inds]), mu_test,
xlab = "predicted", ylab = "actual", main = "Prognostic function")
abline(0,1,col="red",lty=3,lwd=3)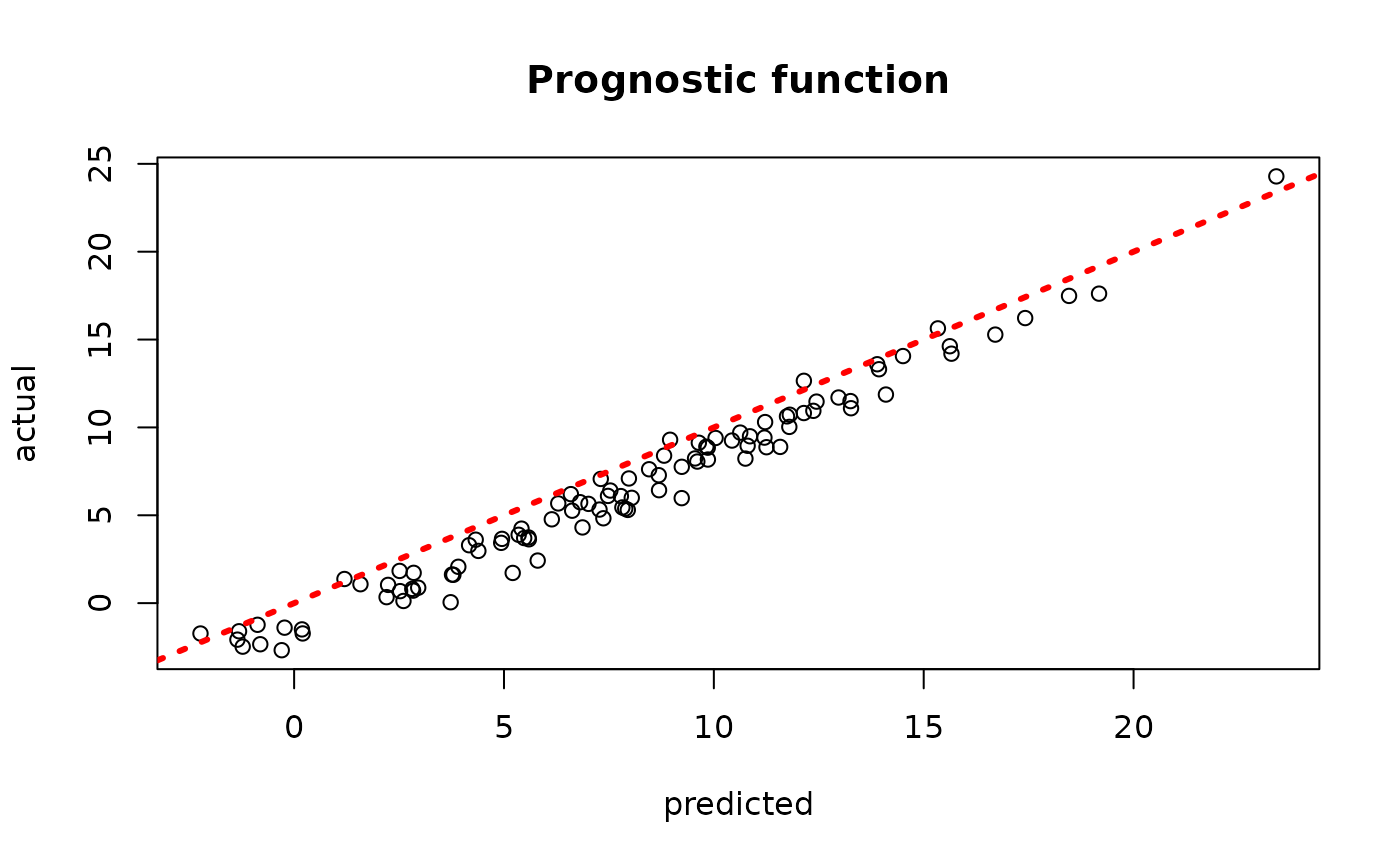
plot(rowMeans(bcf_model_warmstart$tau_hat_test[,sample_inds]), tau_test,
xlab = "predicted", ylab = "actual", main = "Treatment effect")
abline(0,1,col="red",lty=3,lwd=3)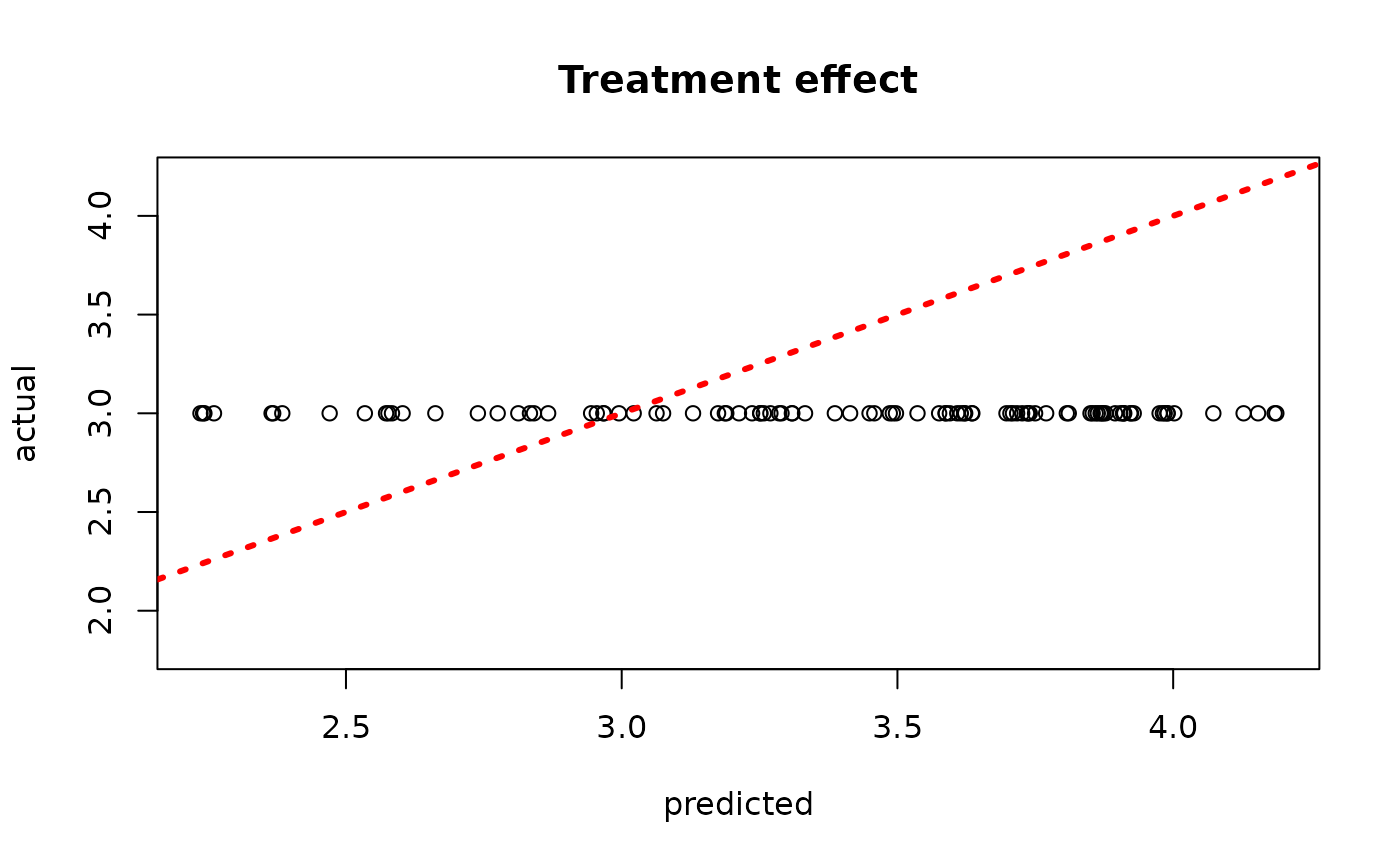
sigma_observed <- var(y-E_XZ)
plot_bounds <- c(min(c(bcf_model_warmstart$sigma2_samples[sample_inds], sigma_observed)),
max(c(bcf_model_warmstart$sigma2_samples[sample_inds], sigma_observed)))
plot(bcf_model_warmstart$sigma2_samples[sample_inds], ylim = plot_bounds,
ylab = "sigma^2", xlab = "Sample", main = "Global variance parameter")
abline(h = sigma_observed, lty=3, lwd = 3, col = "blue")
Examine test set interval coverage
BART MCMC without Warmstart
Next, we simulate from this ensemble model without any warm-start initialization.
num_gfr <- 0
num_burnin <- 100
num_mcmc <- 100
num_samples <- num_gfr + num_burnin + num_mcmc
bcf_model_root <- bcf(
X_train = X_train, Z_train = Z_train, y_train = y_train, pi_train = pi_train,
X_test = X_test, Z_test = Z_test, pi_test = pi_test, feature_types = c(0,0,0,1,1),
num_gfr = num_gfr, num_burnin = num_burnin, num_mcmc = num_mcmc,
sample_sigma_leaf_mu = F, sample_sigma_leaf_tau = F
)Inspect the BART samples after burnin
sample_inds <- (num_burnin+1):num_samples
plot(rowMeans(bcf_model_root$mu_hat_test[,sample_inds]), mu_test,
xlab = "predicted", ylab = "actual", main = "Prognostic function")
abline(0,1,col="red",lty=3,lwd=3)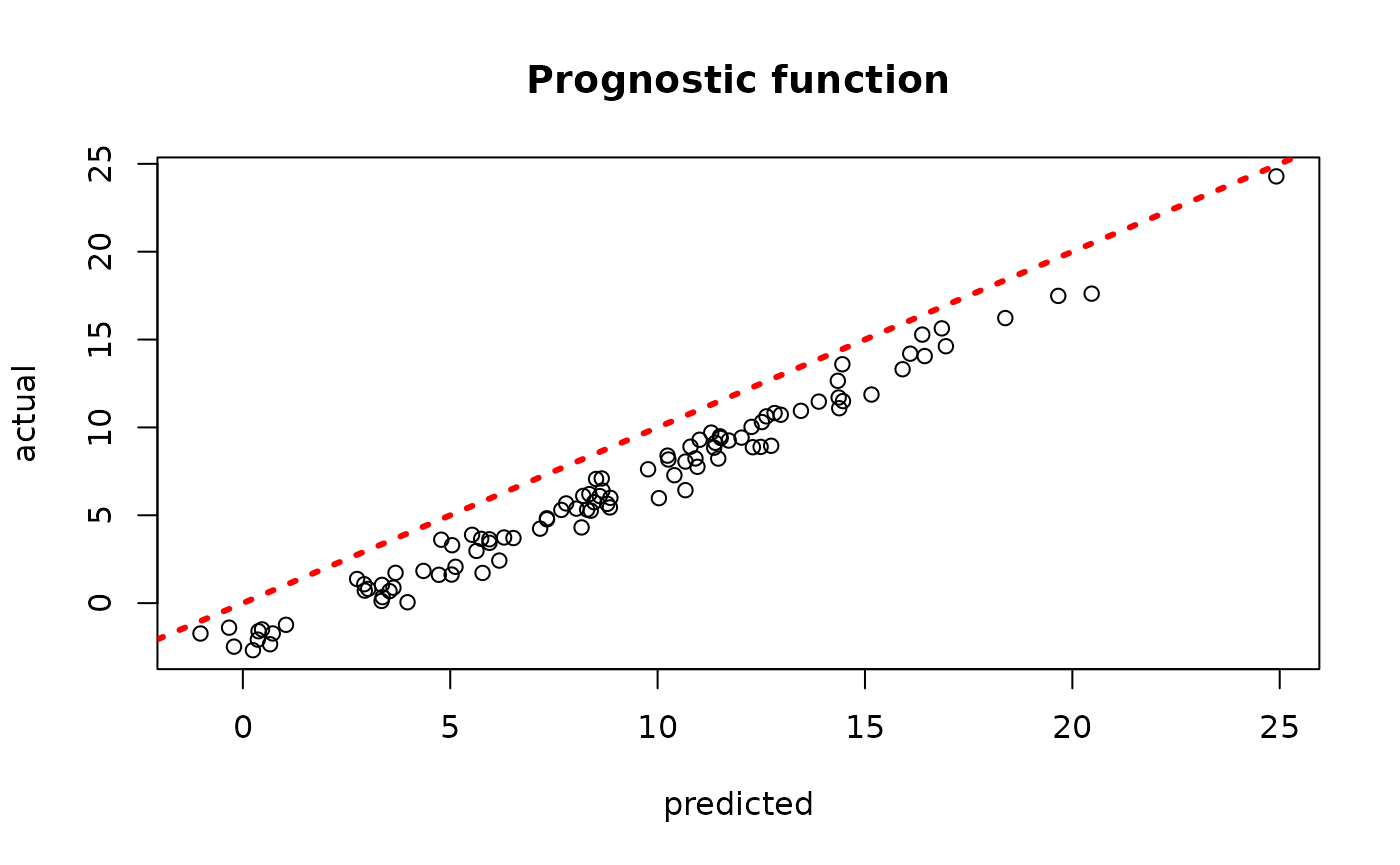
plot(rowMeans(bcf_model_root$tau_hat_test[,sample_inds]), tau_test,
xlab = "predicted", ylab = "actual", main = "Treatment effect")
abline(0,1,col="red",lty=3,lwd=3)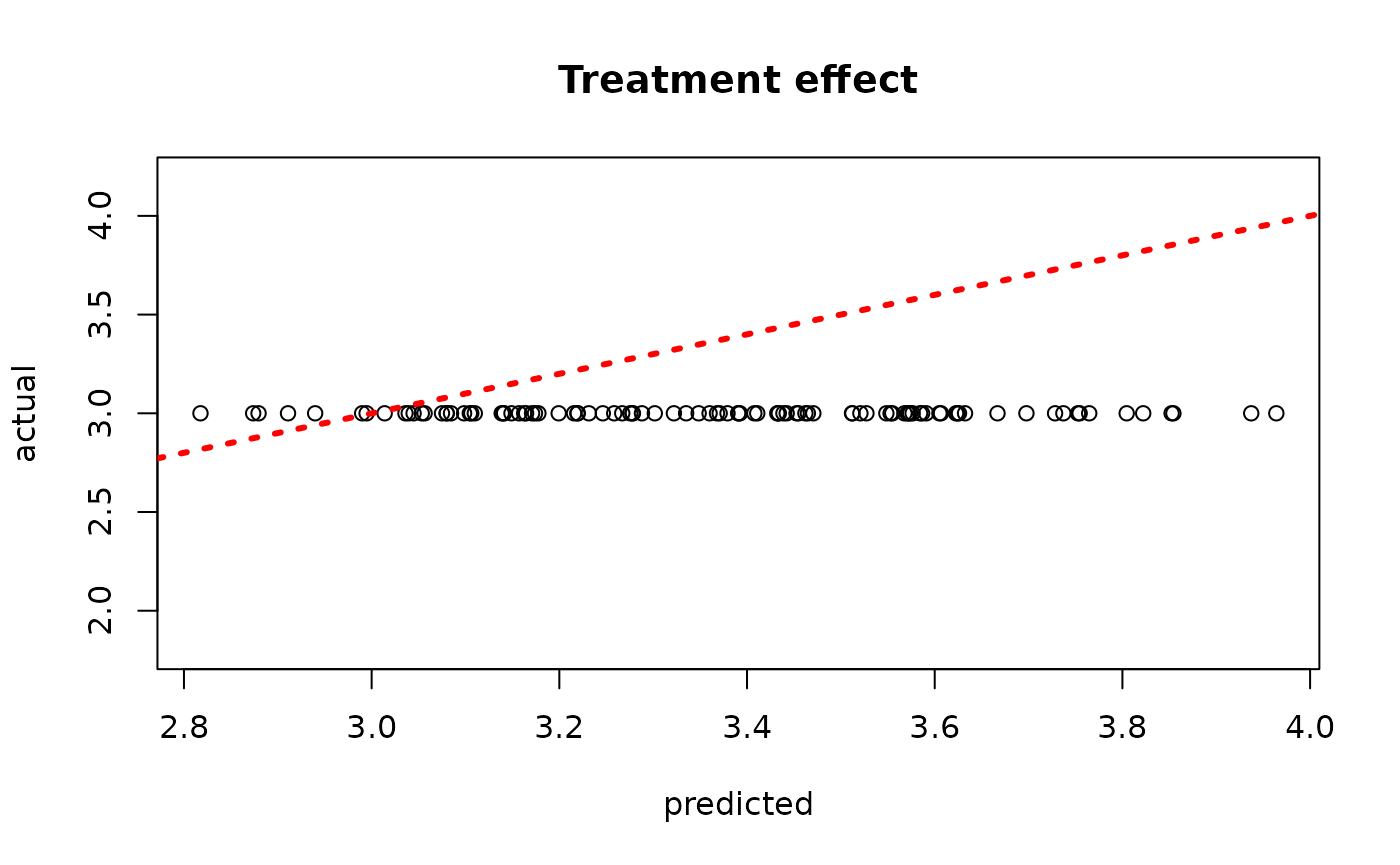
sigma_observed <- var(y-E_XZ)
plot_bounds <- c(min(c(bcf_model_root$sigma2_samples[sample_inds], sigma_observed)),
max(c(bcf_model_root$sigma2_samples[sample_inds], sigma_observed)))
plot(bcf_model_root$sigma2_samples[sample_inds], ylim = plot_bounds,
ylab = "sigma^2", xlab = "Sample", main = "Global variance parameter")
abline(h = sigma_observed, lty=3, lwd = 3, col = "blue")
Examine test set interval coverage
Demo 4: Nonlinear Outcome Model, Heterogeneous Treatment Effect
We consider the following data generating process:
\[\begin{equation*} \begin{aligned} y &= \mu(X) + \tau(X) Z + \epsilon\\ \epsilon &\sim N\left(0,\sigma^2\right)\\ \mu(X) &= \begin{cases} -1.1 & \text{ if} X_1 > X_2\\ 0.9 & \text{ if} X_1 \leq X_2 \end{cases}\\ \tau(X) &= \frac{1}{1+\exp(-X_3)} + \frac{X_2}{10}\\ \pi(X) &= \Phi\left(\mu(X)\right)\\ Z &\sim \text{Bernoulli}\left(\pi(X)\right)\\ X_1,X_2,X_3 &\sim N\left(0,1\right)\\ X_4 &\sim N\left(X_2,1\right)\\ \end{aligned} \end{equation*}\]
Simulation
We draw from the DGP defined above
n <- 1000
x1 <- rnorm(n)
x2 <- rnorm(n)
x3 <- rnorm(n)
x4 <- rnorm(n,x2,1)
X <- cbind(x1,x2,x3,x4)
p <- ncol(X)
mu <- function(x) {-1*(x[,1]>(x[,2])) + 1*(x[,1]<(x[,2])) - 0.1}
tau <- function(x) {1/(1 + exp(-x[,3])) + x[,2]/10}
mu_x <- mu(X)
tau_x <- tau(X)
pi_x <- pnorm(mu_x)
Z <- rbinom(n,1,pi_x)
E_XZ <- mu_x + Z*tau_x
sigma <- diff(range(mu_x + tau_x*pi))/8
y <- E_XZ + sigma*rnorm(n)
# Split data into test and train sets
test_set_pct <- 0.2
n_test <- round(test_set_pct*n)
n_train <- n - n_test
test_inds <- sort(sample(1:n, n_test, replace = F))
train_inds <- (1:n)[!((1:n) %in% test_inds)]
X_test <- X[test_inds,]
X_train <- X[train_inds,]
pi_test <- pi_x[test_inds]
pi_train <- pi_x[train_inds]
Z_test <- Z[test_inds]
Z_train <- Z[train_inds]
y_test <- y[test_inds]
y_train <- y[train_inds]
mu_test <- mu_x[test_inds]
mu_train <- mu_x[train_inds]
tau_test <- tau_x[test_inds]
tau_train <- tau_x[train_inds]Sampling and Analysis
Warmstart
We first simulate from an ensemble model of \(y \mid X\) using “warm-start”
initialization samples (Krantsevich, He, and Hahn
(2023)). This is the default in stochtree.
num_gfr <- 10
num_burnin <- 0
num_mcmc <- 100
num_samples <- num_gfr + num_burnin + num_mcmc
bcf_model_warmstart <- bcf(
X_train = X_train, Z_train = Z_train, y_train = y_train, pi_train = pi_train,
X_test = X_test, Z_test = Z_test, pi_test = pi_test, feature_types = c(0,0,0,1,1),
num_gfr = num_gfr, num_burnin = num_burnin, num_mcmc = num_mcmc,
sample_sigma_leaf_mu = F, sample_sigma_leaf_tau = F
)Inspect the BART samples that were initialized with an XBART warm-start
sample_inds <- (num_gfr+1):num_samples
plot(rowMeans(bcf_model_warmstart$mu_hat_test[,sample_inds]), mu_test,
xlab = "predicted", ylab = "actual", main = "Prognostic function")
abline(0,1,col="red",lty=3,lwd=3)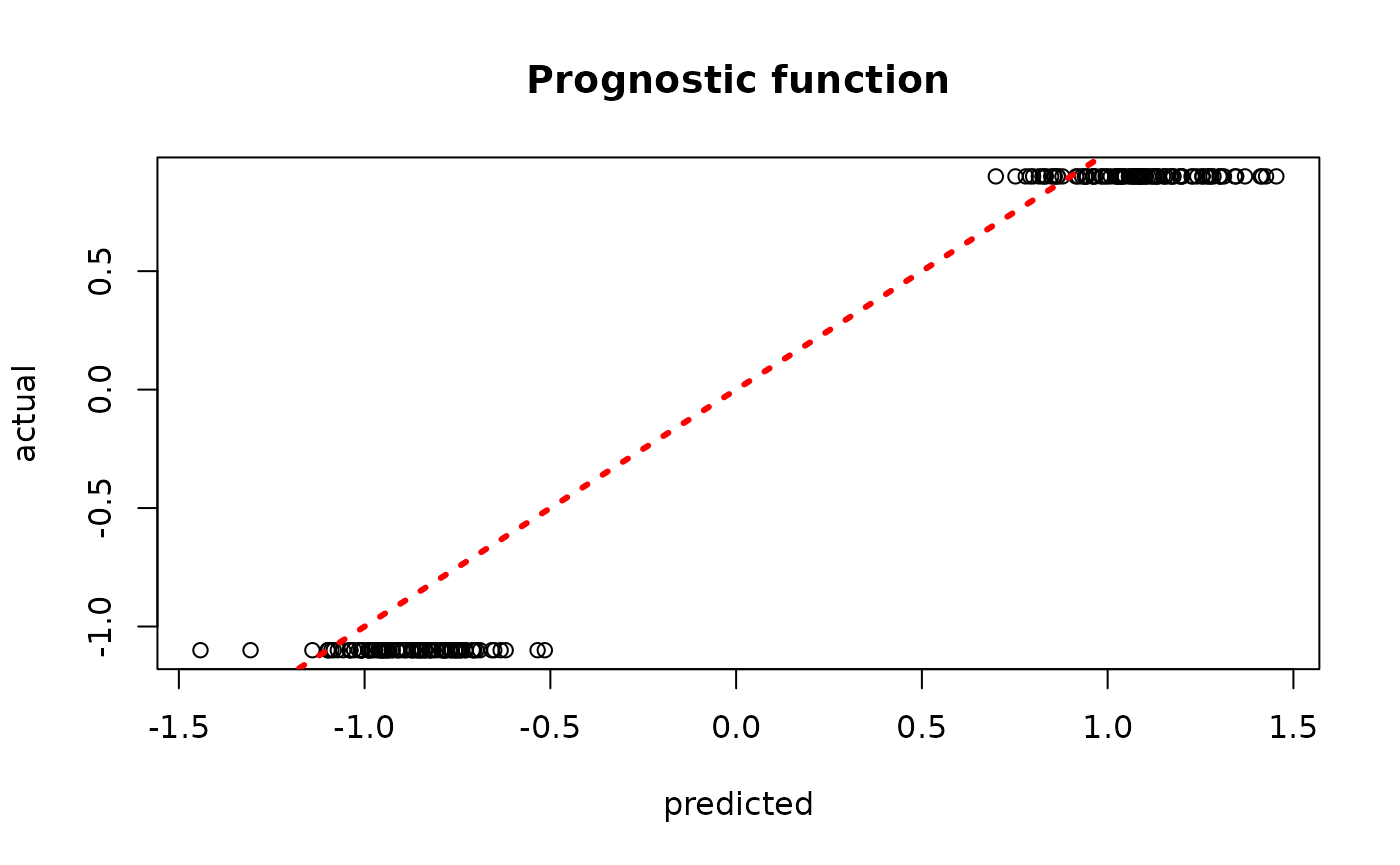
plot(rowMeans(bcf_model_warmstart$tau_hat_test[,sample_inds]), tau_test,
xlab = "predicted", ylab = "actual", main = "Treatment effect")
abline(0,1,col="red",lty=3,lwd=3)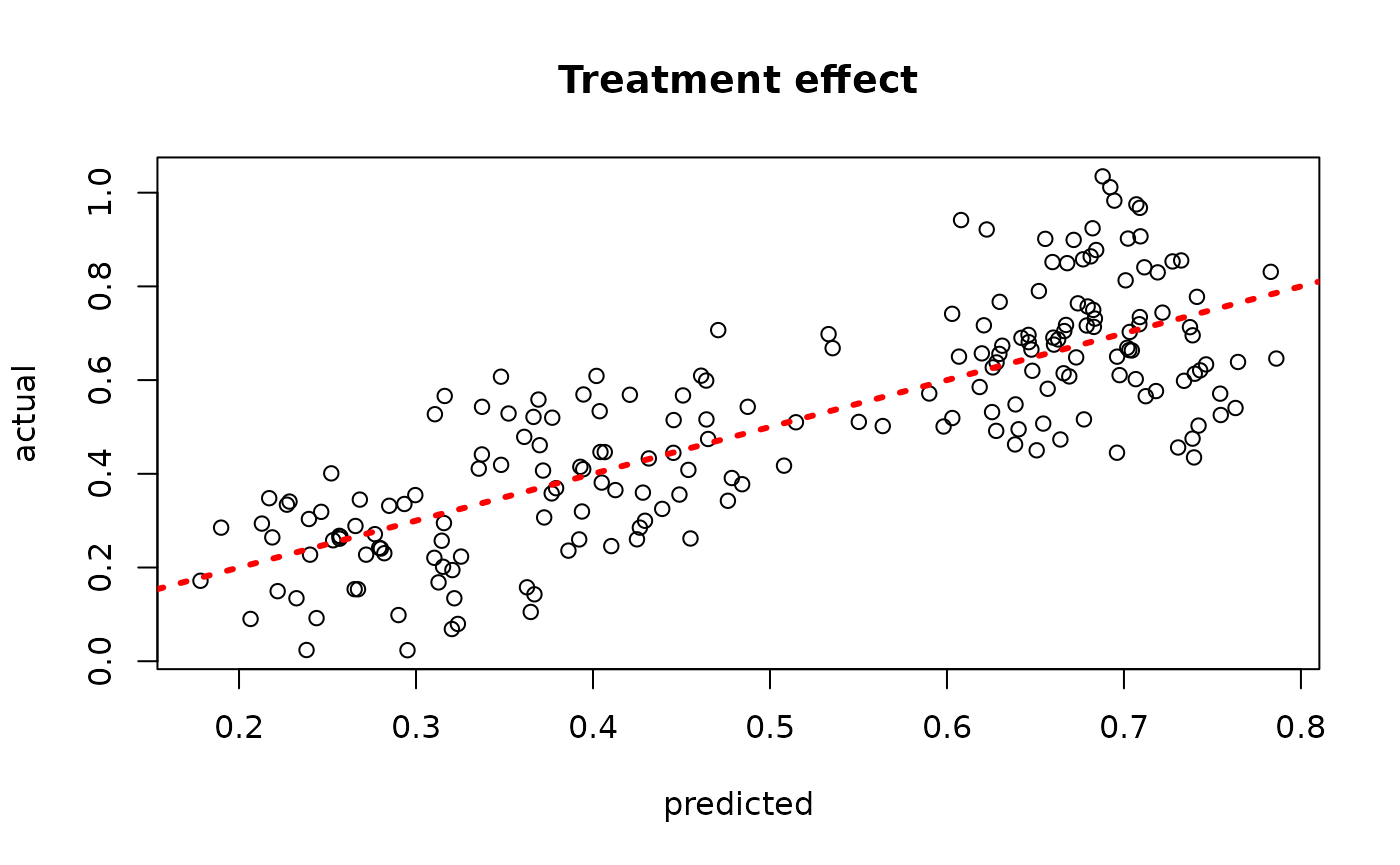
sigma_observed <- var(y-E_XZ)
plot_bounds <- c(min(c(bcf_model_warmstart$sigma2_samples[sample_inds], sigma_observed)),
max(c(bcf_model_warmstart$sigma2_samples[sample_inds], sigma_observed)))
plot(bcf_model_warmstart$sigma2_samples[sample_inds], ylim = plot_bounds,
ylab = "sigma^2", xlab = "Sample", main = "Global variance parameter")
abline(h = sigma_observed, lty=3, lwd = 3, col = "blue")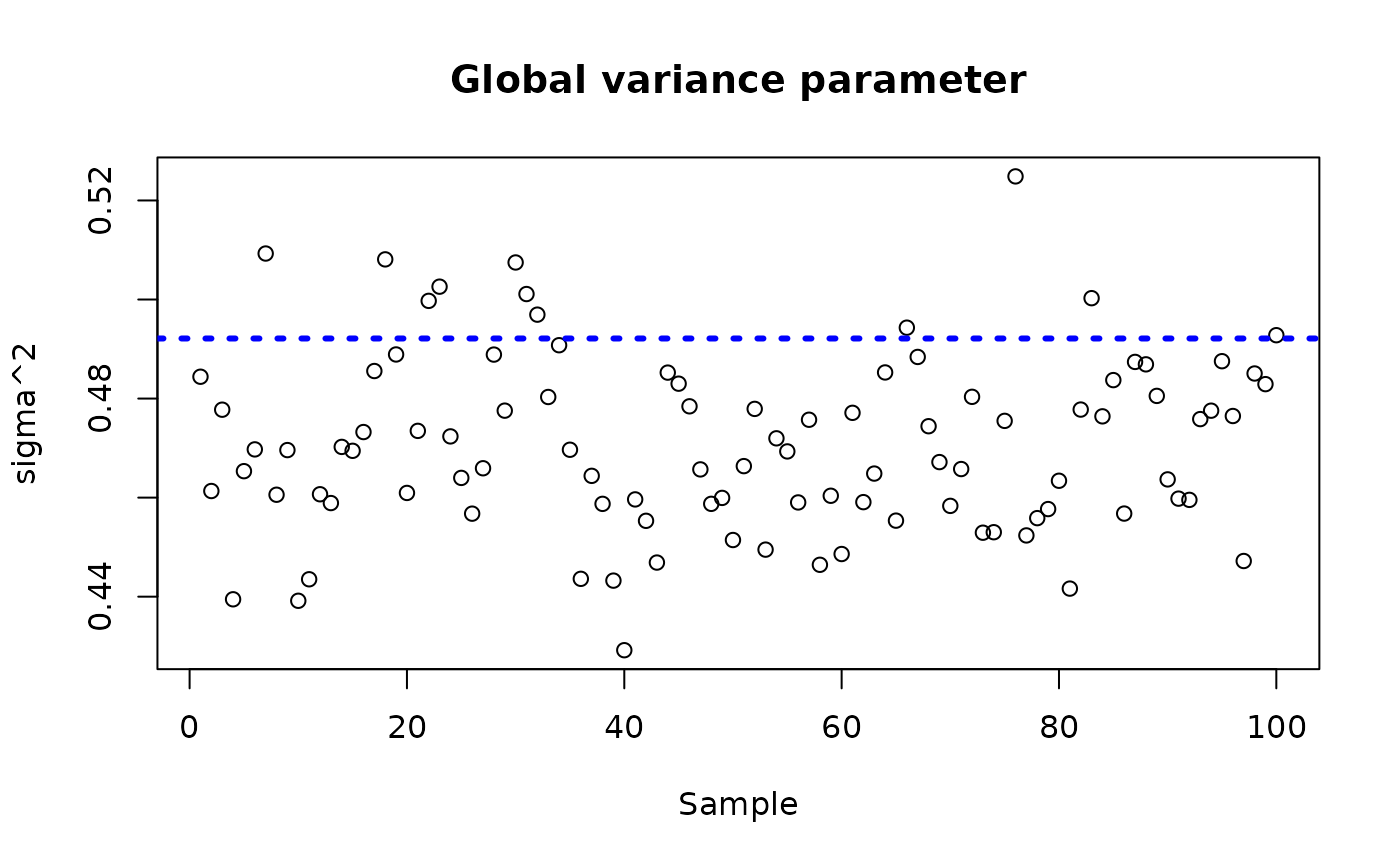
Examine test set interval coverage
BART MCMC without Warmstart
Next, we simulate from this ensemble model without any warm-start initialization.
num_gfr <- 0
num_burnin <- 100
num_mcmc <- 100
num_samples <- num_gfr + num_burnin + num_mcmc
bcf_model_root <- bcf(
X_train = X_train, Z_train = Z_train, y_train = y_train, pi_train = pi_train,
X_test = X_test, Z_test = Z_test, pi_test = pi_test, feature_types = c(0,0,0,1,1),
num_gfr = num_gfr, num_burnin = num_burnin, num_mcmc = num_mcmc,
sample_sigma_leaf_mu = F, sample_sigma_leaf_tau = F
)Inspect the BART samples after burnin
sample_inds <- (num_burnin+1):num_samples
plot(rowMeans(bcf_model_root$mu_hat_test[,sample_inds]), mu_test,
xlab = "predicted", ylab = "actual", main = "Prognostic function")
abline(0,1,col="red",lty=3,lwd=3)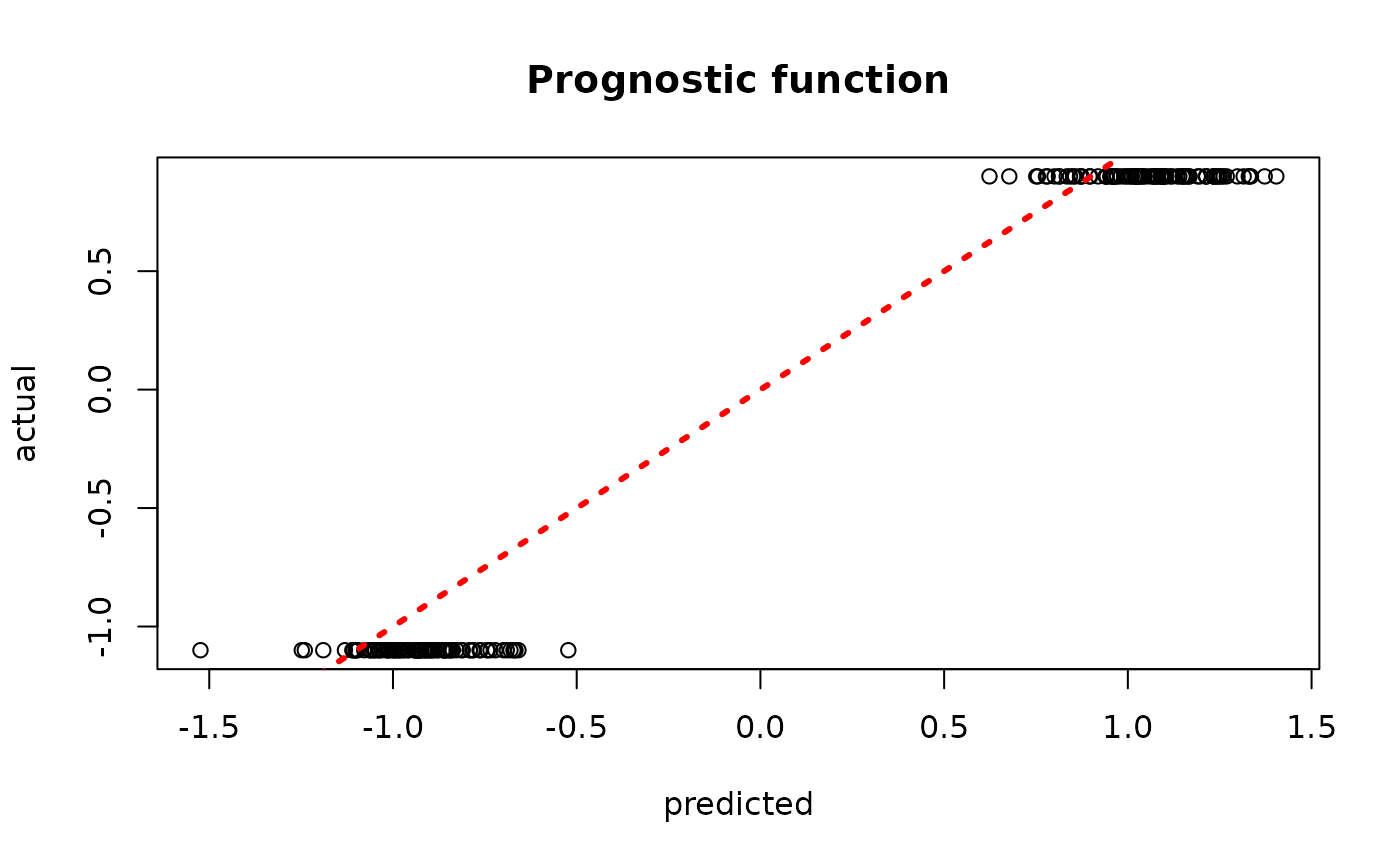
plot(rowMeans(bcf_model_root$tau_hat_test[,sample_inds]), tau_test,
xlab = "predicted", ylab = "actual", main = "Treatment effect")
abline(0,1,col="red",lty=3,lwd=3)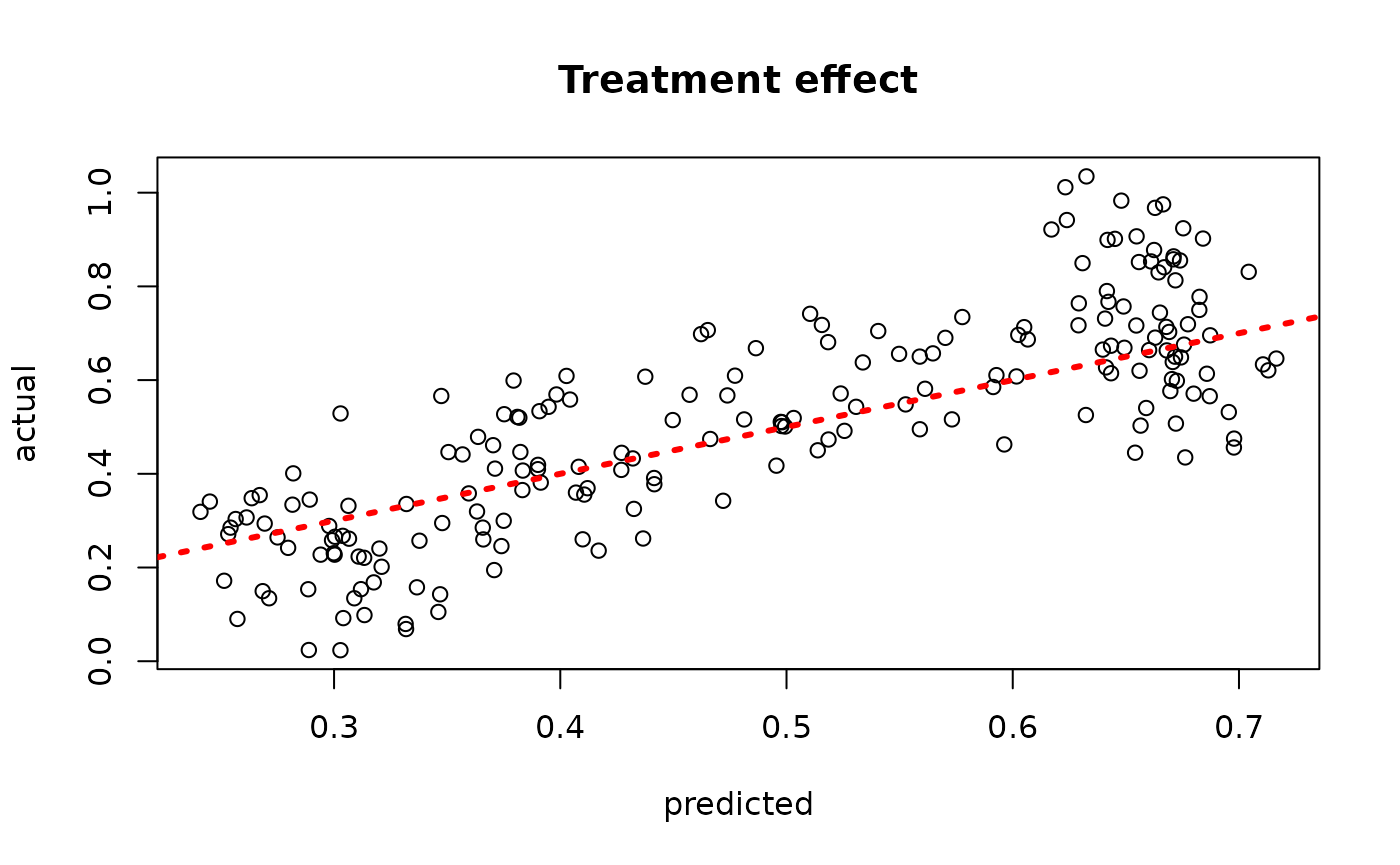
sigma_observed <- var(y-E_XZ)
plot_bounds <- c(min(c(bcf_model_root$sigma2_samples[sample_inds], sigma_observed)),
max(c(bcf_model_root$sigma2_samples[sample_inds], sigma_observed)))
plot(bcf_model_root$sigma2_samples[sample_inds], ylim = plot_bounds,
ylab = "sigma^2", xlab = "Sample", main = "Global variance parameter")
abline(h = sigma_observed, lty=3, lwd = 3, col = "blue")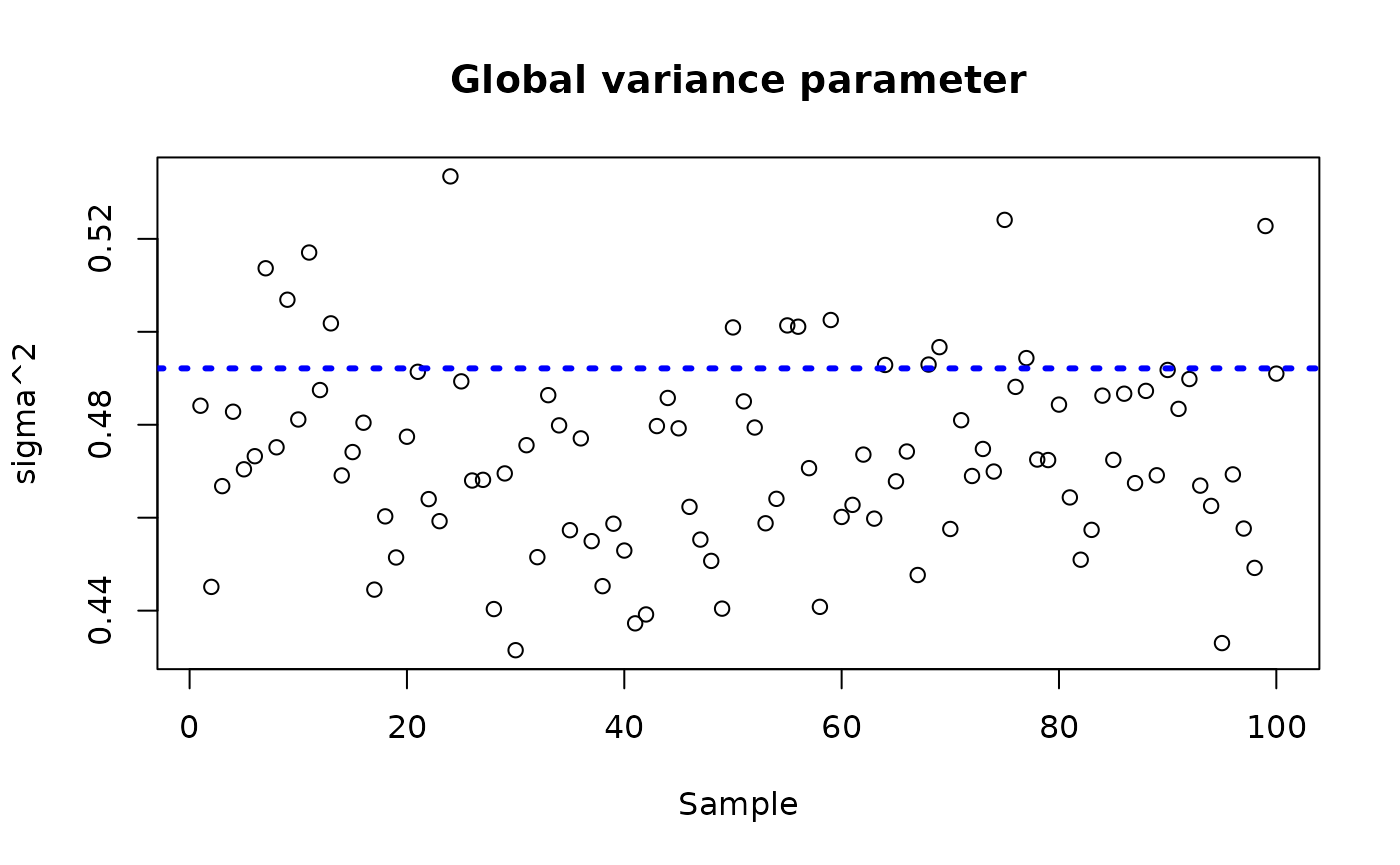
Examine test set interval coverage
Demo 5: Nonlinear Outcome Model, Heterogeneous Treatment Effect with Additive Random Effects
We augment the simulated example in Demo 1 with an additive random
effect structure and show that the bcf() function can
estimate and incorporate these effects into its forest sampling
procedure.
Simulation
We draw from the augmented “demo 1” DGP
n <- 500
snr <- 3
x1 <- rnorm(n)
x2 <- rnorm(n)
x3 <- rnorm(n)
x4 <- as.numeric(rbinom(n,1,0.5))
x5 <- as.numeric(sample(1:3,n,replace=T))
X <- cbind(x1,x2,x3,x4,x5)
p <- ncol(X)
mu_x <- mu1(X)
tau_x <- tau2(X)
pi_x <- 0.8*pnorm((3*mu_x/sd(mu_x)) - 0.5*X[,1]) + 0.05 + runif(n)/10
Z <- rbinom(n,1,pi_x)
E_XZ <- mu_x + Z*tau_x
group_ids <- rep(c(1,2), n %/% 2)
rfx_coefs <- matrix(c(-1, -1, 1, 1),nrow=2,byrow=T)
rfx_basis <- cbind(1, runif(n, -1, 1))
rfx_term <- rowSums(rfx_coefs[group_ids,] * rfx_basis)
y <- E_XZ + rfx_term + rnorm(n, 0, 1)*(sd(E_XZ)/snr)
# Split data into test and train sets
test_set_pct <- 0.2
n_test <- round(test_set_pct*n)
n_train <- n - n_test
test_inds <- sort(sample(1:n, n_test, replace = F))
train_inds <- (1:n)[!((1:n) %in% test_inds)]
X_test <- X[test_inds,]
X_train <- X[train_inds,]
pi_test <- pi_x[test_inds]
pi_train <- pi_x[train_inds]
Z_test <- Z[test_inds]
Z_train <- Z[train_inds]
y_test <- y[test_inds]
y_train <- y[train_inds]
mu_test <- mu_x[test_inds]
mu_train <- mu_x[train_inds]
tau_test <- tau_x[test_inds]
tau_train <- tau_x[train_inds]
group_ids_test <- group_ids[test_inds]
group_ids_train <- group_ids[train_inds]
rfx_basis_test <- rfx_basis[test_inds,]
rfx_basis_train <- rfx_basis[train_inds,]
rfx_term_test <- rfx_term[test_inds]
rfx_term_train <- rfx_term[train_inds]Sampling and Analysis
Warmstart
Here we simulate only from the “warm-start” model (running root-MCMC
BART with random effects is simply a matter of modifying the below code
snippet by setting num_gfr <- 0 and
num_mcmc > 0).
num_gfr <- 100
num_burnin <- 0
num_mcmc <- 500
num_samples <- num_gfr + num_burnin + num_mcmc
bcf_model_warmstart <- bcf(
X_train = X_train, Z_train = Z_train, y_train = y_train, pi_train = pi_train,
group_ids_train = group_ids_train, rfx_basis_train = rfx_basis_train,
X_test = X_test, Z_test = Z_test, pi_test = pi_test, group_ids_test = group_ids_test,
rfx_basis_test = rfx_basis_test, feature_types = c(0,0,0,1,1),
num_gfr = num_gfr, num_burnin = num_burnin, num_mcmc = num_mcmc,
sample_sigma_leaf_mu = T, sample_sigma_leaf_tau = F
)Inspect the BART samples that were initialized with an XBART warm-start
sample_inds <- (num_gfr+1):num_samples
plot(rowMeans(bcf_model_warmstart$mu_hat_test[,sample_inds]), mu_test,
xlab = "predicted", ylab = "actual", main = "Prognostic function")
abline(0,1,col="red",lty=3,lwd=3)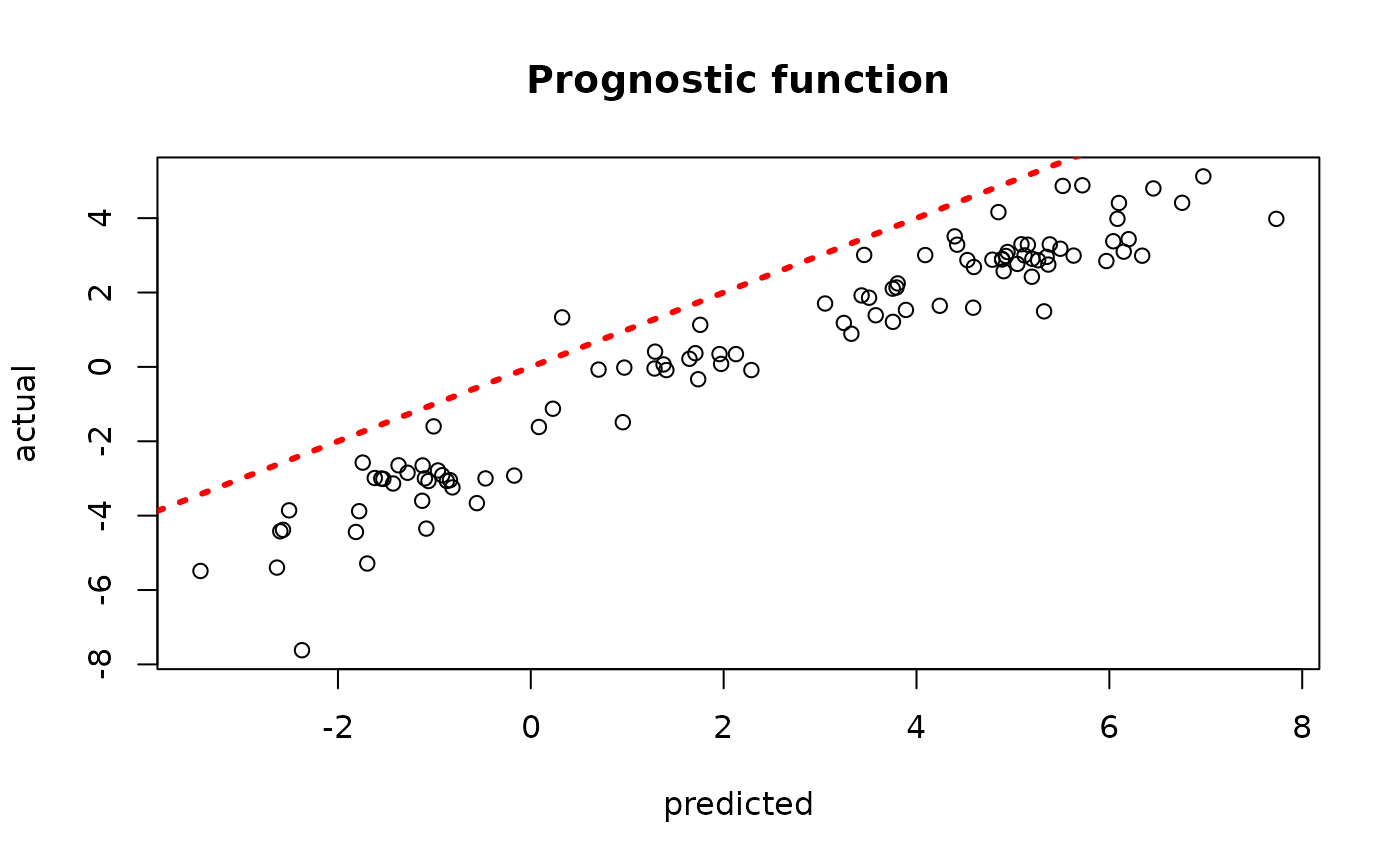
plot(rowMeans(bcf_model_warmstart$tau_hat_test[,sample_inds]), tau_test,
xlab = "predicted", ylab = "actual", main = "Treatment effect")
abline(0,1,col="red",lty=3,lwd=3)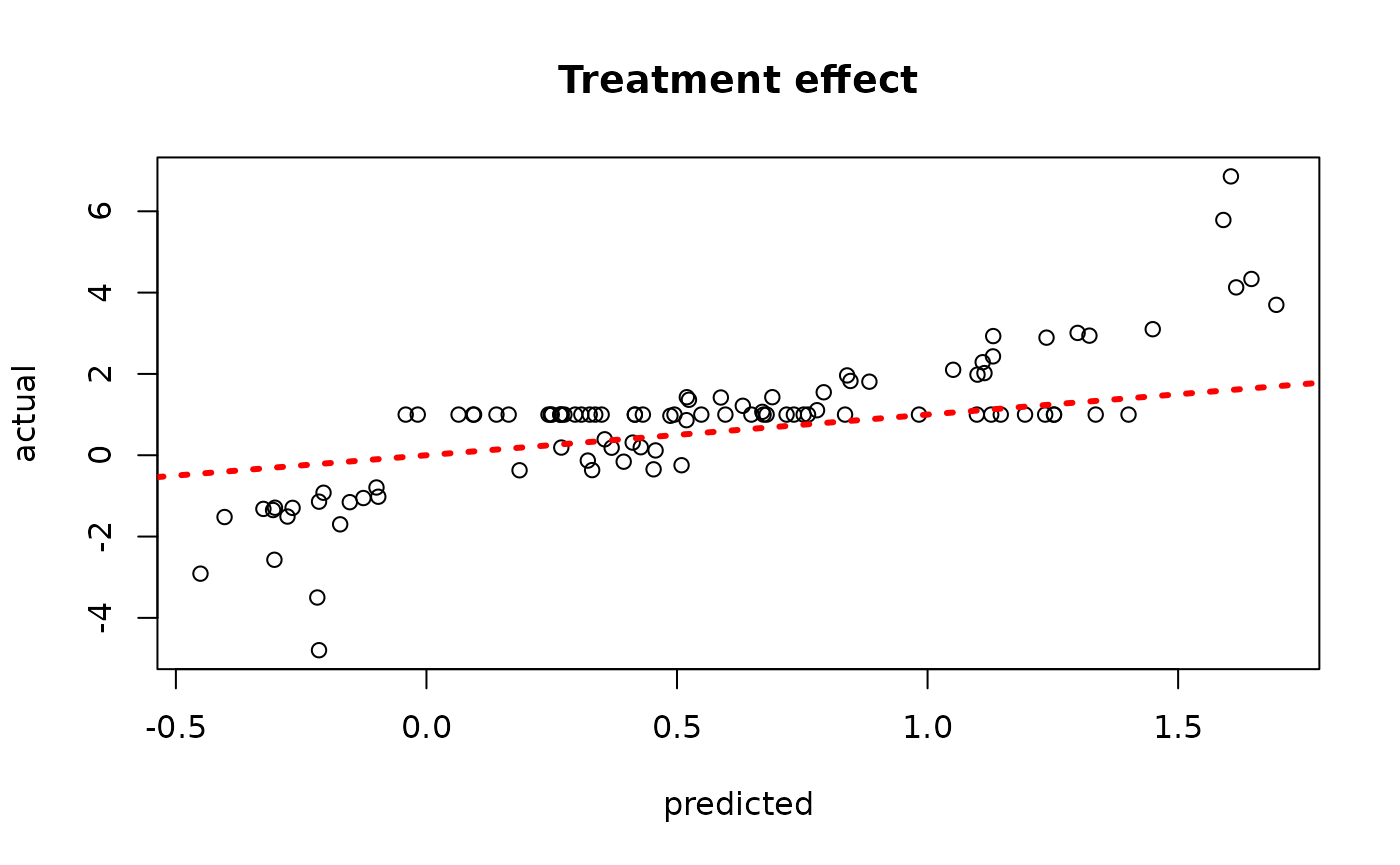
plot(rowMeans(bcf_model_warmstart$y_hat_test[,sample_inds]), y_test,
xlab = "predicted", ylab = "actual", main = "Outcome")
abline(0,1,col="red",lty=3,lwd=3)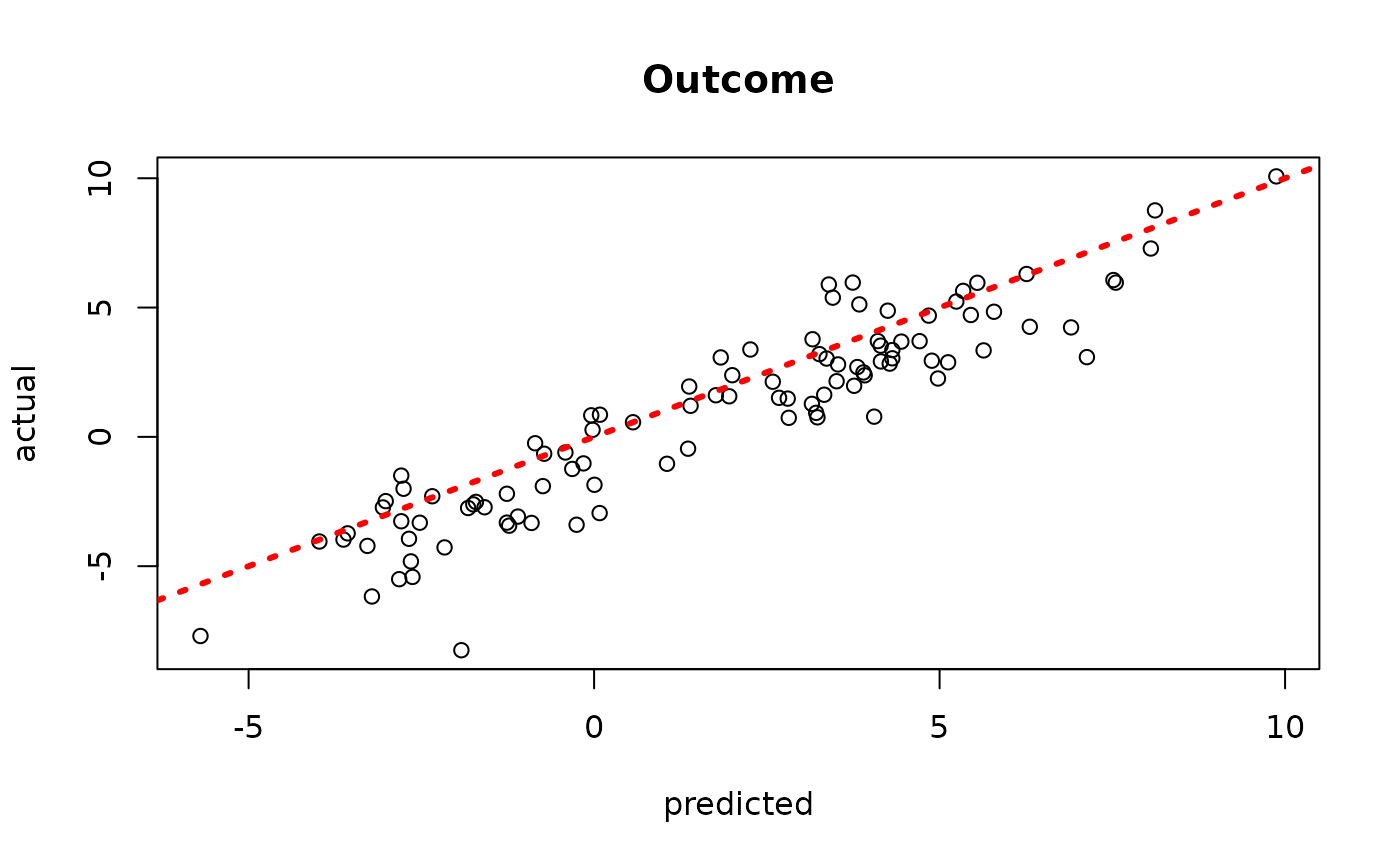
plot(rowMeans(bcf_model_warmstart$rfx_preds_test[,sample_inds]), rfx_term_test,
xlab = "predicted", ylab = "actual", main = "Random effects terms")
abline(0,1,col="red",lty=3,lwd=3)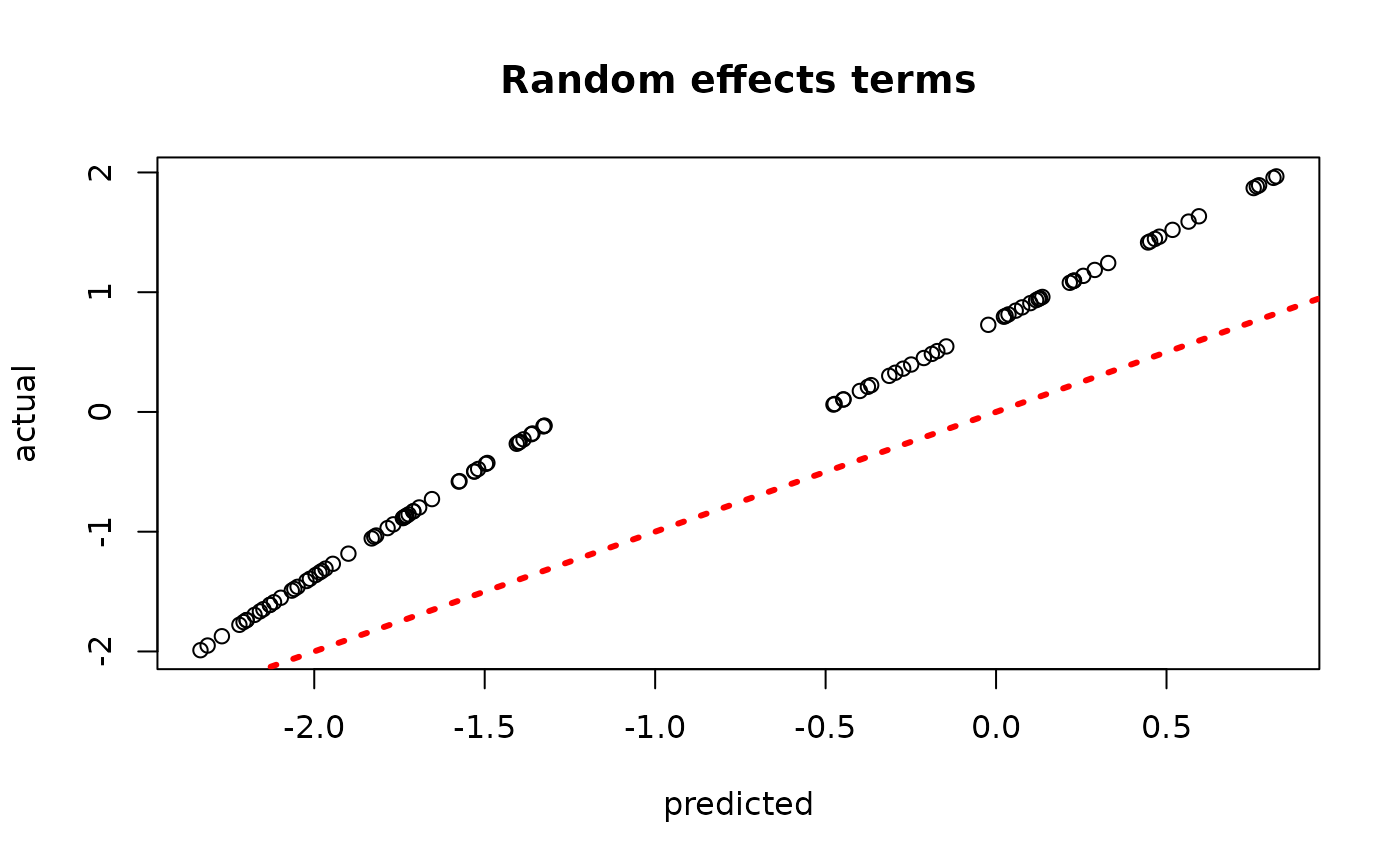
sigma_observed <- var(y-E_XZ-rfx_term)
plot_bounds <- c(min(c(bcf_model_warmstart$sigma2_samples[sample_inds], sigma_observed)),
max(c(bcf_model_warmstart$sigma2_samples[sample_inds], sigma_observed)))
plot(bcf_model_warmstart$sigma2_samples[sample_inds], ylim = plot_bounds,
ylab = "sigma^2", xlab = "Sample", main = "Global variance parameter")
abline(h = sigma_observed, lty=3, lwd = 3, col = "blue")
Examine test set interval coverage
test_lb <- apply(bcf_model_warmstart$tau_hat_test, 1, quantile, 0.025)
test_ub <- apply(bcf_model_warmstart$tau_hat_test, 1, quantile, 0.975)
cover <- (
(test_lb <= tau_x[test_inds]) &
(test_ub >= tau_x[test_inds])
)
mean(cover)
#> [1] 0.91It is clear that causal inference is much more difficult in the presence of both strong covariate-dependent prognostic effects and strong group-level random effects. In this sense, proper prior calibration for all three of the \(\mu\), \(\tau\) and random effects models is crucial.