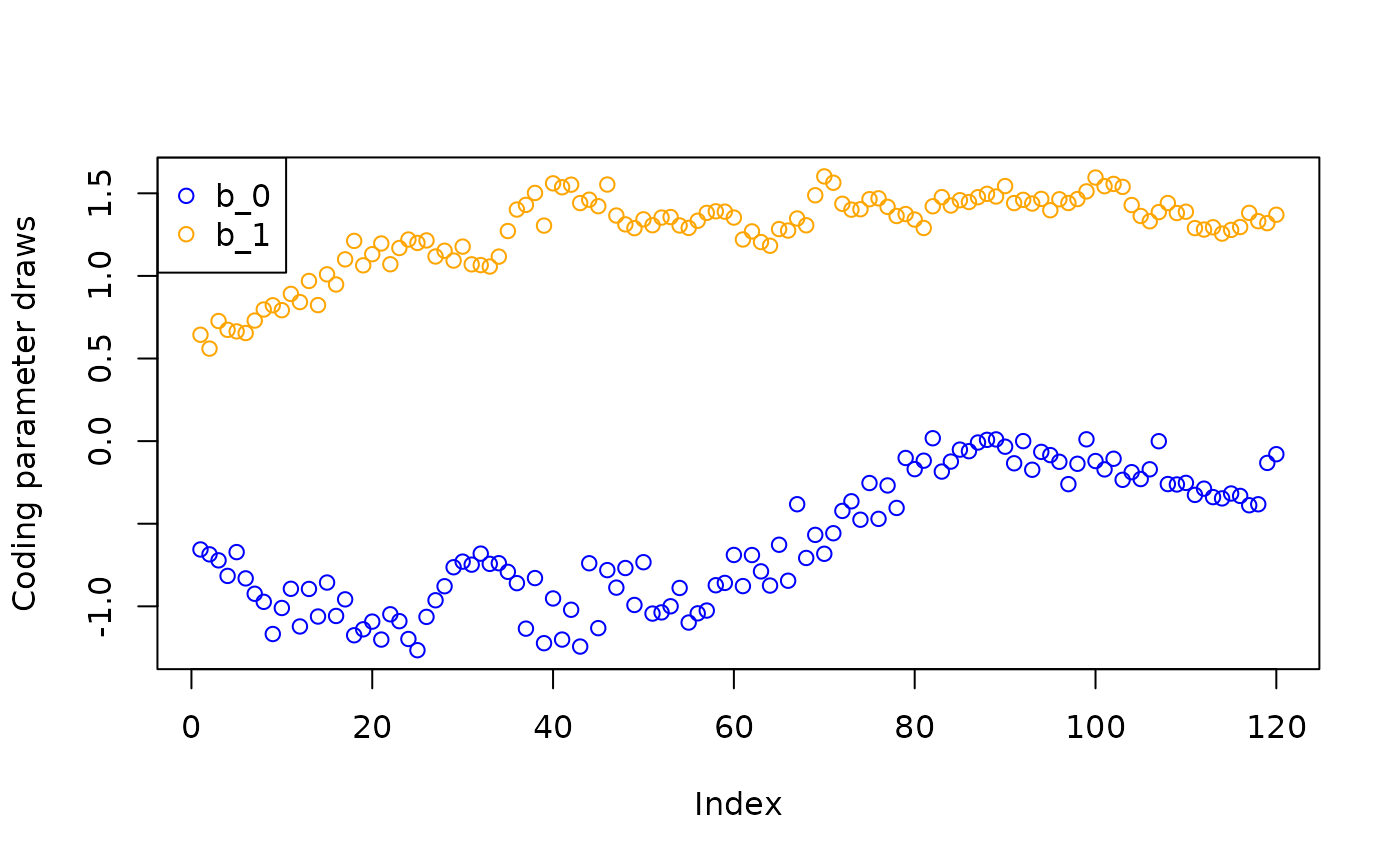Prototype Interface in StochTree

Motivation

While the functions bart() and bcf() provide simple and performant interfaces for supervised learning / causal inference, stochtree also offers access to many of the “low-level” data structures that are typically implemented in C++. This low-level interface is not designed for performance or even simplicity — rather the intent is to provide a “prototype” interface to the C++ code that doesn’t require modifying any C++.

To illustrate when such a prototype interface might be useful, consider the classic BART algorithm:

   INPUT: \(y\), \(X\), \(\tau\), \(\nu\), \(\lambda\), \(\alpha\), \(\beta\)
   OUTPUT: \(m\) samples of a decision forest with \(k\) trees and global variance parameter \(\sigma^2\)
   Initialize \(\sigma^2\) via a default or a data-dependent calibration exercise
   Initialize “forest 0” with \(k\) trees with a single root node, referring to tree \(j\)’s prediction vector as \(f_{0,j}\)
   Compute residual as \(r = y - \sum_{j=1}^k f_{0,j}\)
   FOR \(i\) IN \(\left\{1,\dots,m\right\}\):
      Initialize forest \(i\) from forest \(i-1\)
      FOR \(j\) IN \(\left\{1,\dots,k\right\}\):
         Add predictions for tree \(j\) to residual: \(r = r + f_{i,j}\)
         Update tree \(j\) via Metropolis-Hastings with \(r\) and \(X\) as data and tree priors depending on (\(\tau\), \(\sigma^2\), \(\alpha\), \(\beta\))
         Sample leaf node parameters for tree \(j\) via Gibbs (leaf node prior is \(N\left(0,\tau\right)\))
         Subtract (updated) predictions for tree \(j\) from residual: \(r = r - f_{i,j}\)
      Sample \(\sigma^2\) via Gibbs (prior is \(IG(\nu/2,\nu\lambda/2)\))

While the algorithm itself is conceptually simple, much of the core computation is carried out in low-level languages such as C or C++ because of the tree data structure. As a result, any changes to this algorithm, such as supporting heteroskedasticity (Pratola et al. (2020)), categorical outcomes (Murray (2021)) or causal effect estimation (Hahn, Murray, and Carvalho (2020)) require modifying low-level code.

The prototype interface exposes the core components of the loop above at the R level, thus making it possible to interchange C++ computation for steps like “update tree \(j\) via Metropolis-Hastings” with R computation for a custom variance model, other user-specified additive mean model components, and so on.

To begin, load the stochtree package

library(stochtree)

Demo 1: Supervised Learning

Simulation

Simulate a simple partitioned linear model

# Generate the data
n <- 500
p_X <- 10
p_W <- 1
X <- matrix(runif(n*p_X), ncol = p_X)
W <- matrix(runif(n*p_W), ncol = p_W)
f_XW <- (
    ((0 <= X[,1]) & (0.25 > X[,1])) * (-3*W[,1]) + 
    ((0.25 <= X[,1]) & (0.5 > X[,1])) * (-1*W[,1]) + 
    ((0.5 <= X[,1]) & (0.75 > X[,1])) * (1*W[,1]) + 
    ((0.75 <= X[,1]) & (1 > X[,1])) * (3*W[,1])
)
y <- f_XW + rnorm(n, 0, 1)

# Standardize outcome
y_bar <- mean(y)
y_std <- sd(y)
resid <- (y-y_bar)/y_std

Sampling

Set some parameters that inform the forest and variance parameter samplers

alpha <- 0.9
beta <- 1.25
min_samples_leaf <- 1
num_trees <- 100
cutpoint_grid_size = 100
global_variance_init = 1.
tau_init = 0.5
leaf_prior_scale = matrix(c(tau_init), ncol = 1)
nu <- 4
lambda <- 0.5
a_leaf <- 2.
b_leaf <- 0.5
leaf_regression <- T
feature_types <- as.integer(rep(0, p_X)) # 0 = numeric
var_weights <- rep(1/p_X, p_X)

Initialize R-level access to the C++ classes needed to sample our model

# Data
if (leaf_regression) {
    forest_dataset <- createForestDataset(X, W)
    outcome_model_type <- 1
} else {
    forest_dataset <- createForestDataset(X)
    outcome_model_type <- 0
}
outcome <- createOutcome(resid)

# Random number generator (std::mt19937)
rng <- createRNG()

# Sampling data structures
forest_model <- createForestModel(forest_dataset, feature_types, 
                                  num_trees, n, alpha, beta, min_samples_leaf)

# Container of forest samples
if (leaf_regression) {
    forest_samples <- createForestContainer(num_trees, 1, F)
} else {
    forest_samples <- createForestContainer(num_trees, 1, T)
}

Prepare to run the sampler

num_warmstart <- 10
num_mcmc <- 100
num_samples <- num_warmstart + num_mcmc
global_var_samples <- c(global_variance_init, rep(0, num_samples))
leaf_scale_samples <- c(tau_init, rep(0, num_samples))

Run the grow-from-root sampler to “warm-start” BART

for (i in 1:num_warmstart) {
    # Sample forest
    forest_model$sample_one_iteration(
        forest_dataset, outcome, forest_samples, rng, feature_types, 
        outcome_model_type, leaf_prior_scale, var_weights, 
        global_var_samples[i], cutpoint_grid_size, gfr = T
    )
    
    # Sample global variance parameter
    global_var_samples[i+1] <- sample_sigma2_one_iteration(
        outcome, rng, nu, lambda
    )
    
    # Sample leaf node variance parameter and update `leaf_prior_scale`
    leaf_scale_samples[i+1] <- sample_tau_one_iteration(
        forest_samples, rng, a_leaf, b_leaf, i-1
    )
    leaf_prior_scale[1,1] <- leaf_scale_samples[i+1]
}

Pick up from the last GFR forest (and associated global variance / leaf scale parameters) with an MCMC sampler

for (i in (num_warmstart+1):num_samples) {
    # Sample forest
    forest_model$sample_one_iteration(
        forest_dataset, outcome, forest_samples, rng, feature_types, 
        outcome_model_type, leaf_prior_scale, var_weights, 
        global_var_samples[i], cutpoint_grid_size, gfr = F
    )
    
    # Sample global variance parameter
    global_var_samples[i+1] <- sample_sigma2_one_iteration(
        outcome, rng, nu, lambda
    )
    
    # Sample leaf node variance parameter and update `leaf_prior_scale`
    leaf_scale_samples[i+1] <- sample_tau_one_iteration(
        forest_samples, rng, a_leaf, b_leaf, i-1
    )
    leaf_prior_scale[1,1] <- leaf_scale_samples[i+1]
}

Predict and rescale samples

# Forest predictions
preds <- forest_samples$predict(forest_dataset)*y_std + y_bar

# Global error variance
sigma_samples <- sqrt(global_var_samples)*y_std

Results

Inspect the initial samples obtained via “grow-from-root” (He and Hahn (2023))

plot(sigma_samples[1:num_warmstart], ylab="sigma")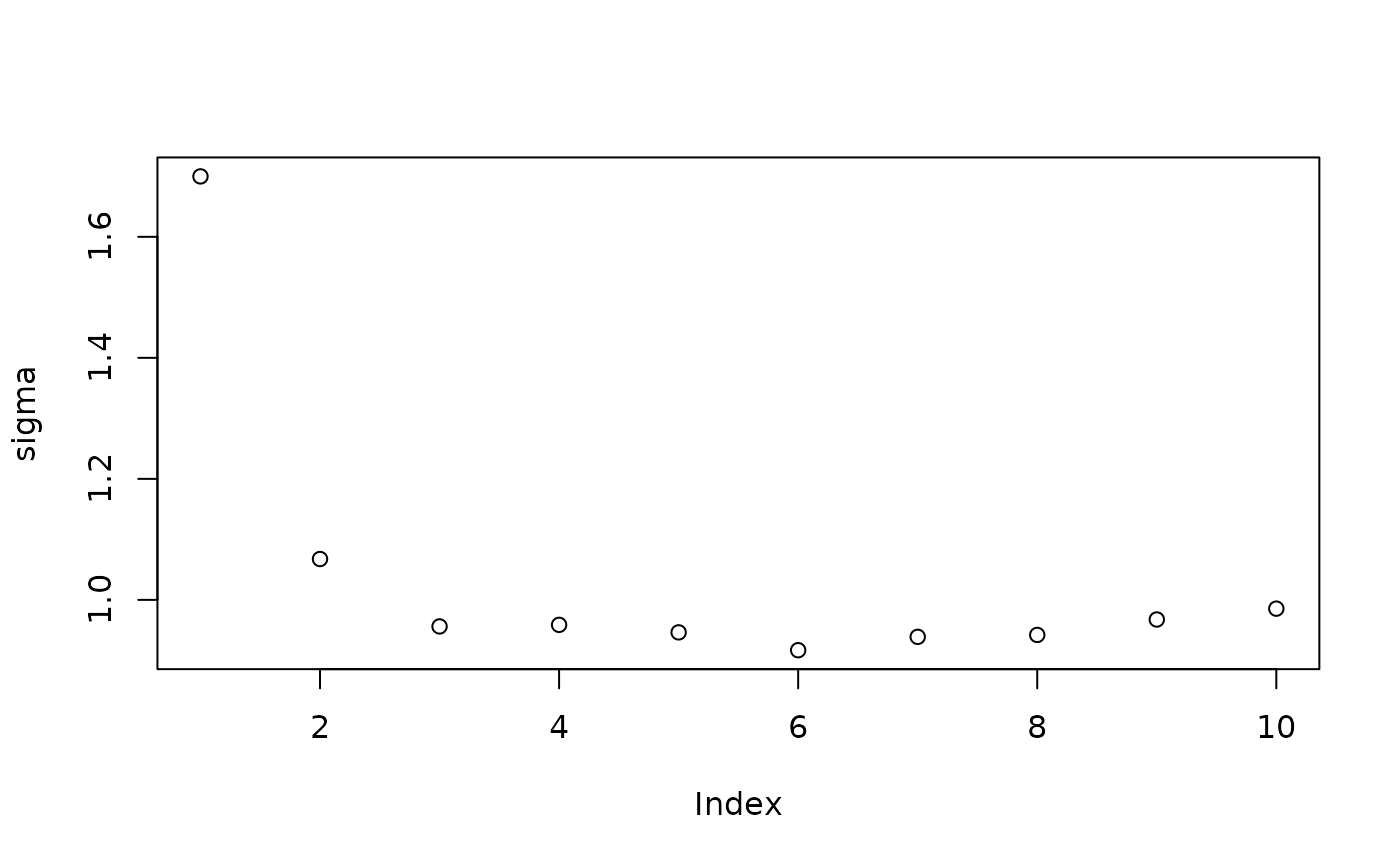

plot(rowMeans(preds[,1:num_warmstart]), y, pch=16, 
     cex=0.75, xlab = "pred", ylab = "actual")
abline(0,1,col="red",lty=2,lwd=2.5)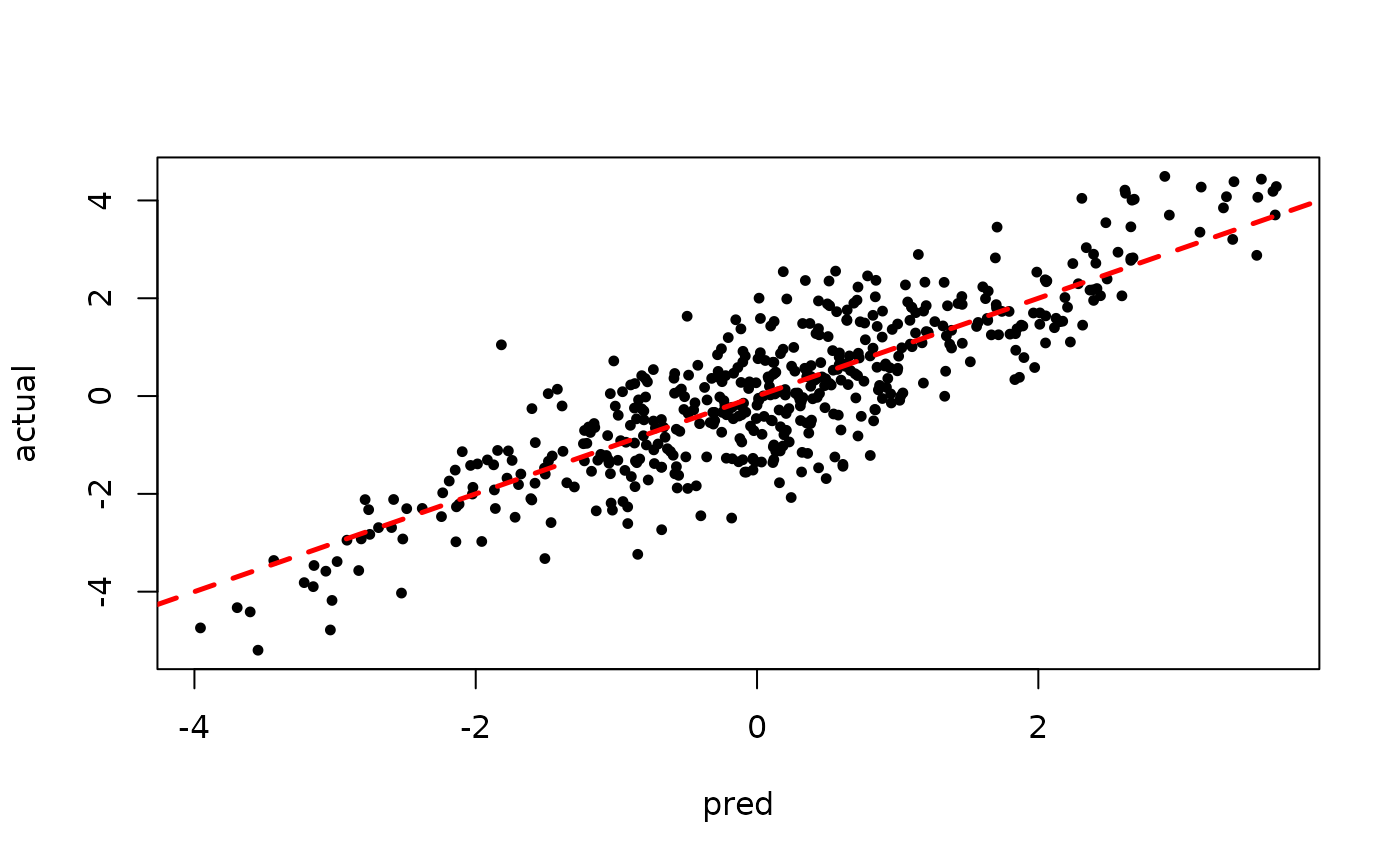

Inspect the BART samples obtained after “warm-starting”

plot(sigma_samples[(num_warmstart+1):num_samples], ylab="sigma")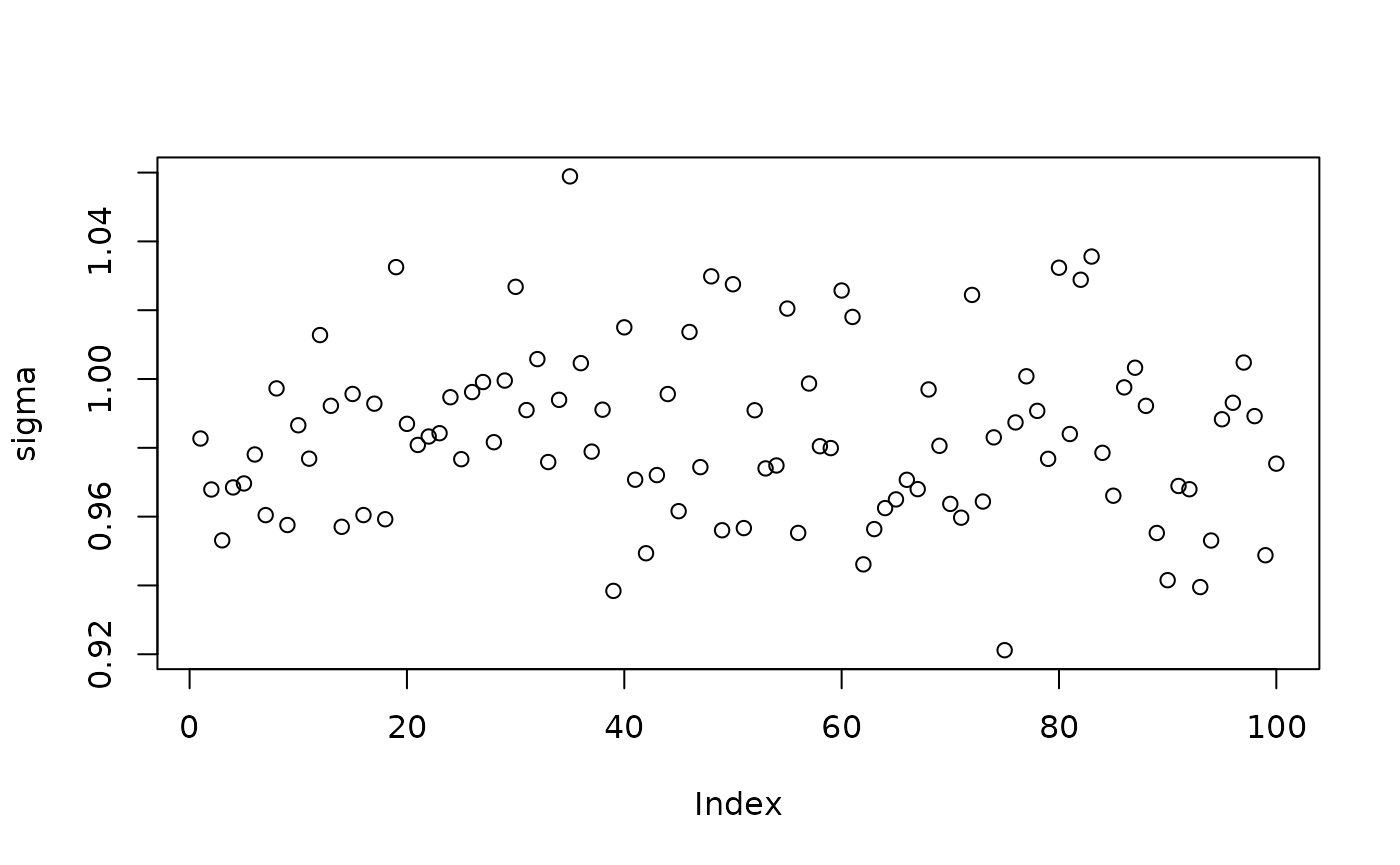

plot(rowMeans(preds[,(num_warmstart+1):num_samples]), y, pch=16, 
     cex=0.75, xlab = "pred", ylab = "actual")
abline(0,1,col="red",lty=2,lwd=2.5)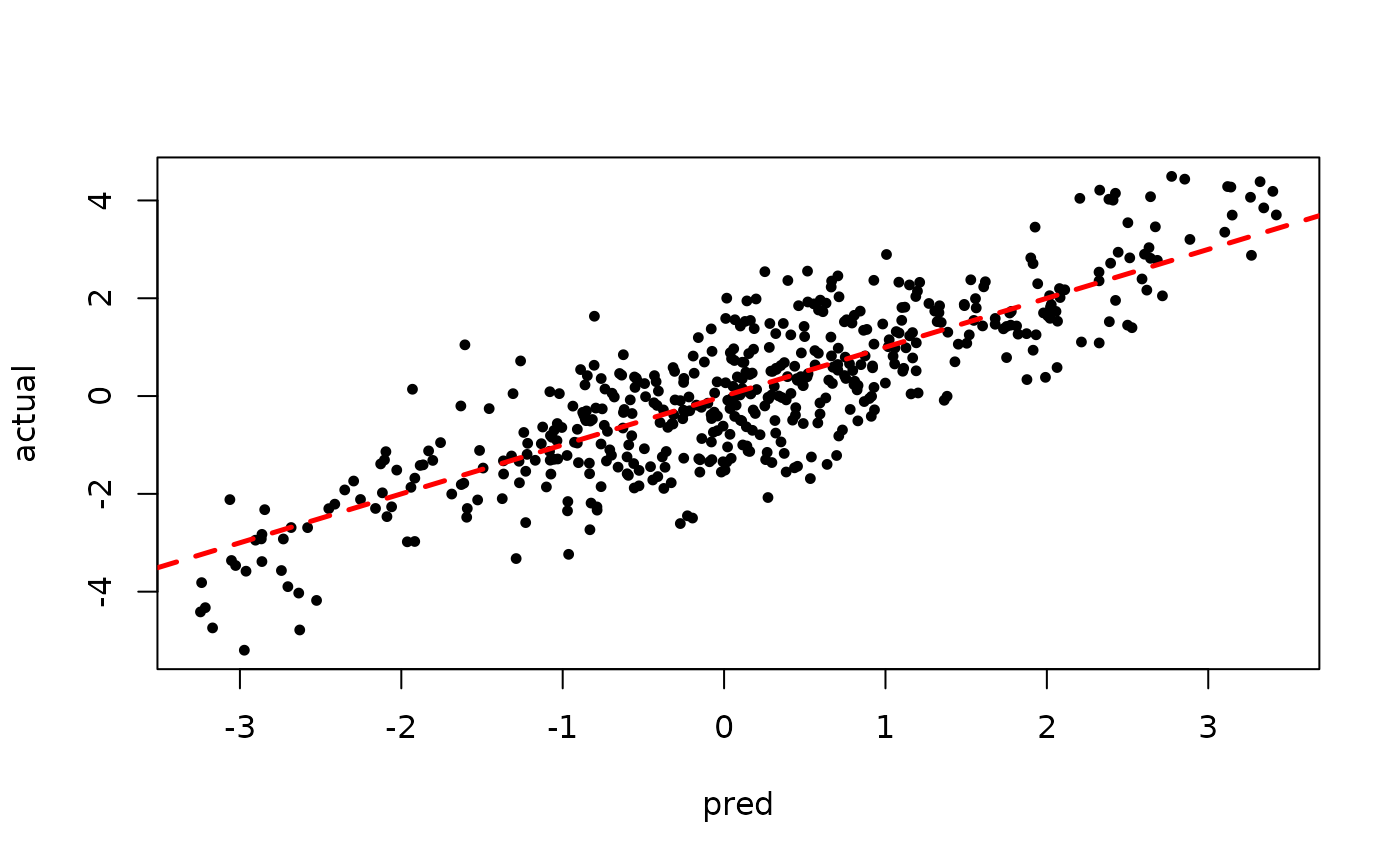

Demo 2: Supervised Learning with Additive Random Effects

We build on the above example and add a simple “random effects” structure: every observation is in either group 1 or group 2 and there is a random group intercept (simulated to be quite strong, underscoring the need for random effects modeling).

Simulation

Simulate a partitioned linear model with a simple additive group random effect structure

# Generate the data
n <- 500
p_X <- 10
p_W <- 1
X <- matrix(runif(n*p_X), ncol = p_X)
W <- matrix(runif(n*p_W), ncol = p_W)
group_ids <- rep(c(1,2), n %/% 2)
rfx_coefs <- c(-5, 5)
rfx_basis <- rep(1, n)
f_XW <- (
    ((0 <= X[,1]) & (0.25 > X[,1])) * (-3*W[,1]) + 
    ((0.25 <= X[,1]) & (0.5 > X[,1])) * (-1*W[,1]) + 
    ((0.5 <= X[,1]) & (0.75 > X[,1])) * (1*W[,1]) + 
    ((0.75 <= X[,1]) & (1 > X[,1])) * (3*W[,1])
)
rfx_term <- rfx_coefs[group_ids] * rfx_basis
y <- f_XW + rfx_term + rnorm(n, 0, 1)

# Standardize outcome
y_bar <- mean(y)
y_std <- sd(y)
resid <- (y-y_bar)/y_std

Sampling

Set some parameters that inform the forest and variance parameter samplers

alpha <- 0.9
beta <- 1.25
min_samples_leaf <- 1
num_trees <- 100
cutpoint_grid_size = 100
global_variance_init = 1.
tau_init = 0.5
leaf_prior_scale = matrix(c(tau_init), ncol = 1)
nu <- 4
lambda <- 0.5
a_leaf <- 2.
b_leaf <- 0.5
leaf_regression <- T
feature_types <- as.integer(rep(0, p_X)) # 0 = numeric
var_weights <- rep(1/p_X, p_X)

Set some parameters that inform the random effects samplers

alpha_init <- c(1)
xi_init <- matrix(c(1,1),1,2)
sigma_alpha_init <- matrix(c(1),1,1)
sigma_xi_init <- matrix(c(1),1,1)
sigma_xi_shape <- 1
sigma_xi_scale <- 1

Initialize R-level access to the C++ classes needed to sample our model

# Data
if (leaf_regression) {
    forest_dataset <- createForestDataset(X, W)
    outcome_model_type <- 1
} else {
    forest_dataset <- createForestDataset(X)
    outcome_model_type <- 0
}
outcome <- createOutcome(resid)

# Random number generator (std::mt19937)
rng <- createRNG()

# Sampling data structures
forest_model <- createForestModel(forest_dataset, feature_types, 
                                  num_trees, n, alpha, beta, min_samples_leaf)

# Container of forest samples
if (leaf_regression) {
    forest_samples <- createForestContainer(num_trees, 1, F)
} else {
    forest_samples <- createForestContainer(num_trees, 1, T)
}

# Random effects dataset
rfx_basis <- as.matrix(rfx_basis)
group_ids <- as.integer(group_ids)
rfx_dataset <- createRandomEffectsDataset(group_ids, rfx_basis)

# Random effects details
num_groups <- length(unique(group_ids))
num_components <- ncol(rfx_basis)

# Random effects tracker
rfx_tracker <- createRandomEffectsTracker(group_ids)

# Random effects model
rfx_model <- createRandomEffectsModel(num_components, num_groups)
rfx_model$set_working_parameter(alpha_init)
rfx_model$set_group_parameters(xi_init)
rfx_model$set_working_parameter_cov(sigma_alpha_init)
rfx_model$set_group_parameter_cov(sigma_xi_init)
rfx_model$set_variance_prior_shape(sigma_xi_shape)
rfx_model$set_variance_prior_scale(sigma_xi_scale)

# Random effect samples
rfx_samples <- createRandomEffectSamples(num_components, num_groups, rfx_tracker)

Prepare to run the sampler

num_warmstart <- 10
num_mcmc <- 100
num_samples <- num_warmstart + num_mcmc
global_var_samples <- c(global_variance_init, rep(0, num_samples))
leaf_scale_samples <- c(tau_init, rep(0, num_samples))

Run the grow-from-root sampler to “warm-start” BART

for (i in 1:num_warmstart) {
    # Sample forest
    forest_model$sample_one_iteration(
        forest_dataset, outcome, forest_samples, rng, feature_types, 
        outcome_model_type, leaf_prior_scale, var_weights, 
        global_var_samples[i], cutpoint_grid_size, gfr = T
    )
    
    # Sample global variance parameter
    global_var_samples[i+1] <- sample_sigma2_one_iteration(
        outcome, rng, nu, lambda
    )
    
    # Sample leaf node variance parameter and update `leaf_prior_scale`
    leaf_scale_samples[i+1] <- sample_tau_one_iteration(
        forest_samples, rng, a_leaf, b_leaf, i-1
    )
    leaf_prior_scale[1,1] <- leaf_scale_samples[i+1]
    
    # Sample random effects model
    rfx_model$sample_random_effect(rfx_dataset, outcome, rfx_tracker, rfx_samples, global_var_samples[i+1], rng)
}

Pick up from the last GFR forest (and associated global variance / leaf scale parameters) with an MCMC sampler

for (i in (num_warmstart+1):num_samples) {
    # Sample forest
    forest_model$sample_one_iteration(
        forest_dataset, outcome, forest_samples, rng, feature_types, 
        outcome_model_type, leaf_prior_scale, var_weights, 
        global_var_samples[i], cutpoint_grid_size, gfr = F
    )
    
    # Sample global variance parameter
    global_var_samples[i+1] <- sample_sigma2_one_iteration(
        outcome, rng, nu, lambda
    )
    
    # Sample leaf node variance parameter and update `leaf_prior_scale`
    leaf_scale_samples[i+1] <- sample_tau_one_iteration(
        forest_samples, rng, a_leaf, b_leaf, i-1
    )
    leaf_prior_scale[1,1] <- leaf_scale_samples[i+1]
    
    # Sample random effects model
    rfx_model$sample_random_effect(rfx_dataset, outcome, rfx_tracker, rfx_samples, global_var_samples[i+1], rng)
}

Predict and rescale samples

# Forest predictions
forest_preds <- forest_samples$predict(forest_dataset)*y_std + y_bar

# Random effects predictions
rfx_preds <- rfx_samples$predict(group_ids, rfx_basis)*y_std

# Overall predictions
preds <- forest_preds + rfx_preds

# Global error variance
sigma_samples <- sqrt(global_var_samples)*y_std

Results

Inspect the initial samples obtained via grow-from-root and an additive random effects model

plot(sigma_samples[1:num_warmstart], ylab="sigma")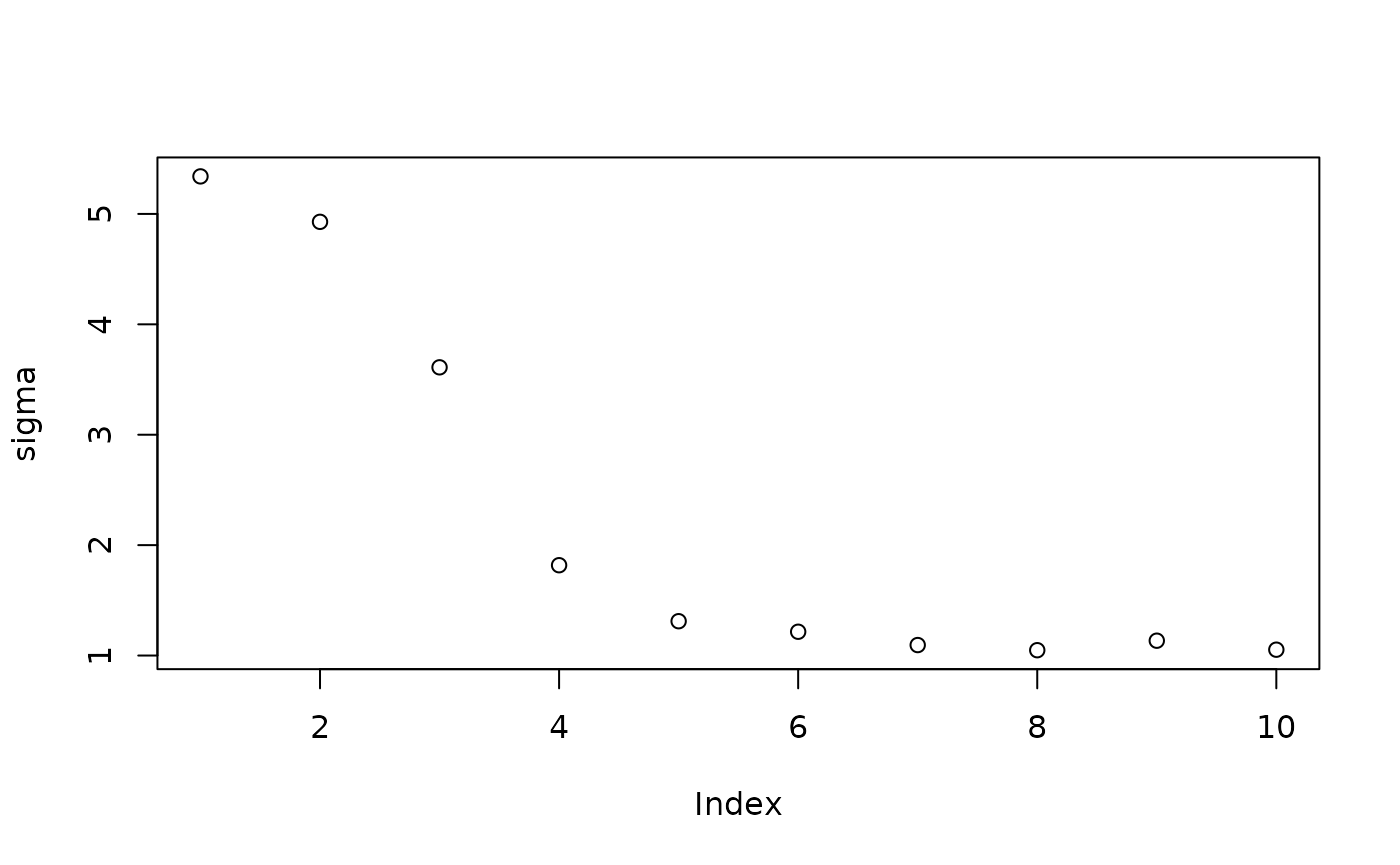

plot(rowMeans(preds[,1:num_warmstart]), y, pch=16, 
     cex=0.75, xlab = "pred", ylab = "actual")
abline(0,1,col="red",lty=2,lwd=2.5)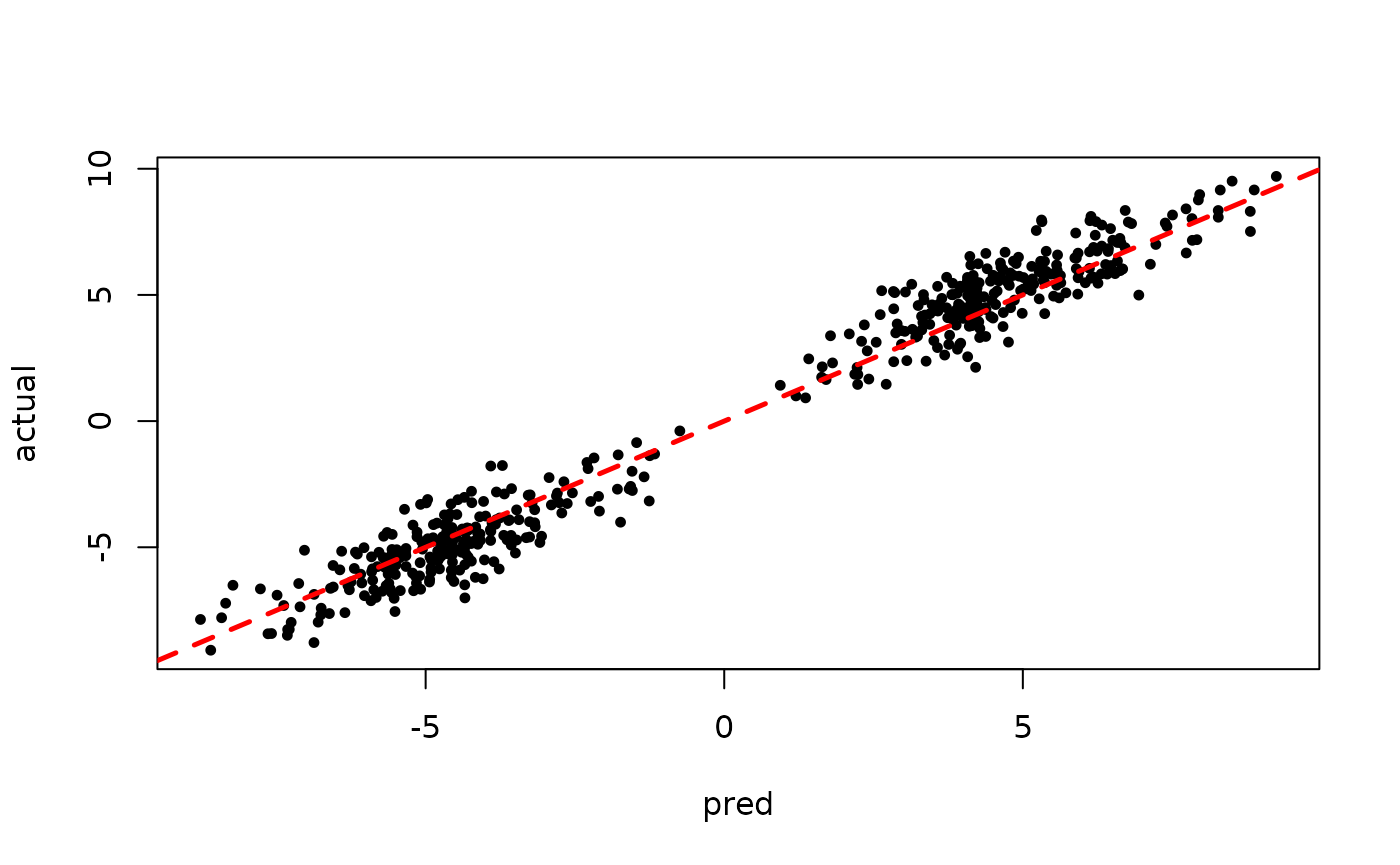

Inspect the BART samples obtained after “warm-starting” plus an additive random effects model

plot(sigma_samples[(num_warmstart+1):num_samples], ylab="sigma")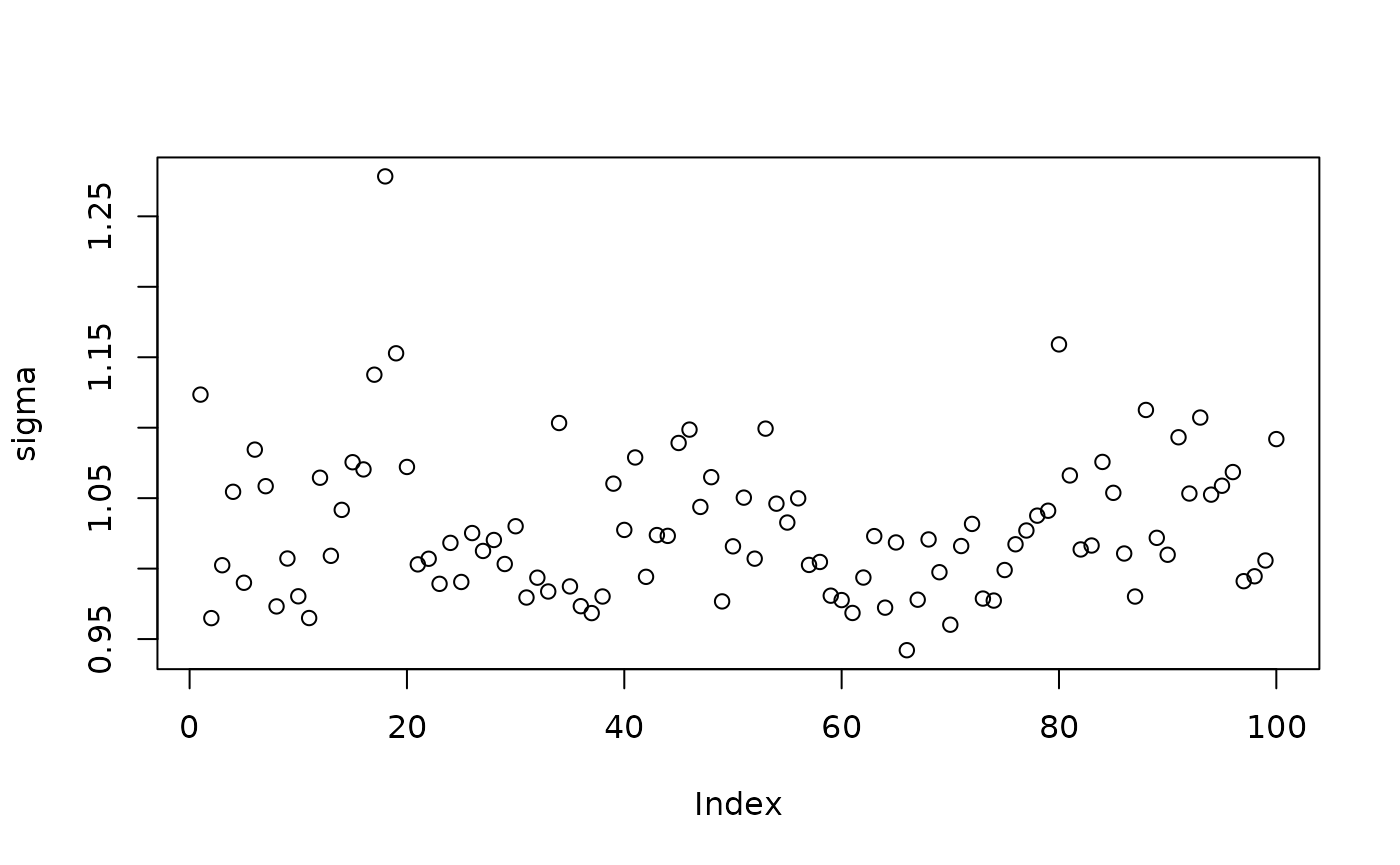

plot(rowMeans(preds[,(num_warmstart+1):num_samples]), y, pch=16, 
     cex=0.75, xlab = "pred", ylab = "actual")
abline(0,1,col="red",lty=2,lwd=2.5)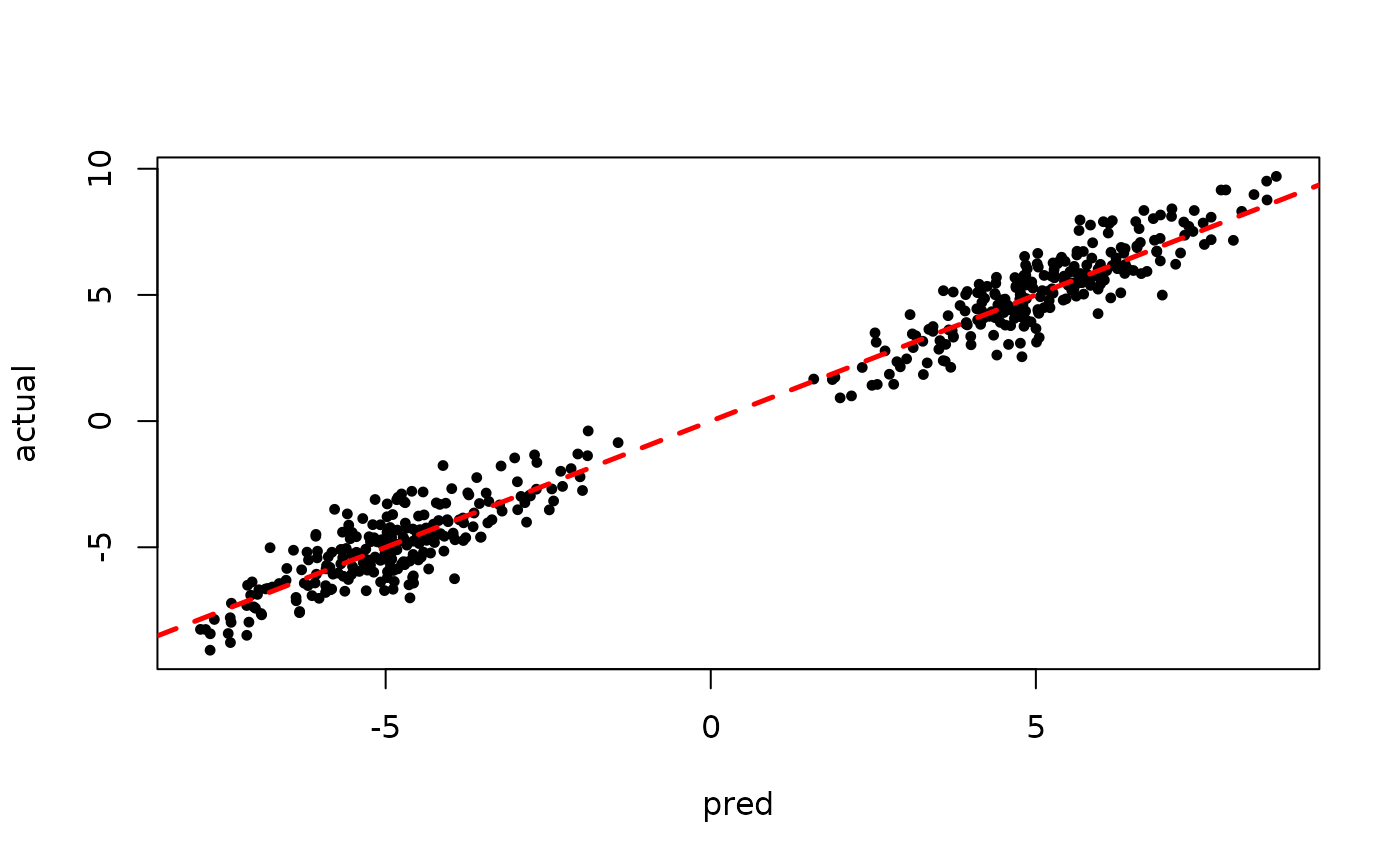

Now inspect the samples from the BART forest alone (without considering the random effect predictions)

plot(rowMeans(forest_preds[,(num_warmstart+1):num_samples]), y, pch=16, 
     cex=0.75, xlab = "pred", ylab = "actual")
abline(0,1,col="red",lty=2,lwd=2.5)

Demo 3: Supervised Learning with Additive Multi-Component Random Effects

We build once again on the above example, in this case allowing for a random intercept and regression coefficient (on a pre-specified basis) for each group (1 and 2).

Simulation

Simulate a partitioned linear model with a simple additive group random effect structure

# Generate the data
n <- 500
p_X <- 10
p_W <- 1
X <- matrix(runif(n*p_X), ncol = p_X)
W <- matrix(runif(n*p_W), ncol = p_W)
group_ids <- rep(c(1,2), n %/% 2)
rfx_coefs <- matrix(c(-5, -3, 5, 3),nrow=2,byrow=T)
rfx_basis <- cbind(1, runif(n, -1, 1))
f_XW <- (
    ((0 <= X[,1]) & (0.25 > X[,1])) * (-3*W[,1]) + 
    ((0.25 <= X[,1]) & (0.5 > X[,1])) * (-1*W[,1]) + 
    ((0.5 <= X[,1]) & (0.75 > X[,1])) * (1*W[,1]) + 
    ((0.75 <= X[,1]) & (1 > X[,1])) * (3*W[,1])
)
rfx_term <- rowSums(rfx_coefs[group_ids,] * rfx_basis)
y <- f_XW + rfx_term + rnorm(n, 0, 1)

# Standardize outcome
y_bar <- mean(y)
y_std <- sd(y)
resid <- (y-y_bar)/y_std

Sampling

Set some parameters that inform the forest and variance parameter samplers

alpha <- 0.9
beta <- 1.25
min_samples_leaf <- 1
num_trees <- 100
cutpoint_grid_size = 100
global_variance_init = 1.
tau_init = 0.5
leaf_prior_scale = matrix(c(tau_init), ncol = 1)
nu <- 4
lambda <- 0.5
a_leaf <- 2.
b_leaf <- 0.5
leaf_regression <- T
feature_types <- as.integer(rep(0, p_X)) # 0 = numeric
var_weights <- rep(1/p_X, p_X)

Set some parameters that inform the random effects samplers

alpha_init <- c(1,0)
xi_init <- matrix(c(1,0,1,0),2,2)
sigma_alpha_init <- diag(1,2,2)
sigma_xi_init <- diag(1,2,2)
sigma_xi_shape <- 1
sigma_xi_scale <- 1

Initialize R-level access to the C++ classes needed to sample our model

# Data
if (leaf_regression) {
    forest_dataset <- createForestDataset(X, W)
    outcome_model_type <- 1
} else {
    forest_dataset <- createForestDataset(X)
    outcome_model_type <- 0
}
outcome <- createOutcome(resid)

# Random number generator (std::mt19937)
rng <- createRNG()

# Sampling data structures
forest_model <- createForestModel(forest_dataset, feature_types, 
                                  num_trees, n, alpha, beta, min_samples_leaf)

# Container of forest samples
if (leaf_regression) {
    forest_samples <- createForestContainer(num_trees, 1, F)
} else {
    forest_samples <- createForestContainer(num_trees, 1, T)
}

# Random effects dataset
rfx_basis <- as.matrix(rfx_basis)
group_ids <- as.integer(group_ids)
rfx_dataset <- createRandomEffectsDataset(group_ids, rfx_basis)

# Random effects details
num_groups <- length(unique(group_ids))
num_components <- ncol(rfx_basis)

# Random effects tracker
rfx_tracker <- createRandomEffectsTracker(group_ids)

# Random effects model
rfx_model <- createRandomEffectsModel(num_components, num_groups)
rfx_model$set_working_parameter(alpha_init)
rfx_model$set_group_parameters(xi_init)
rfx_model$set_working_parameter_cov(sigma_alpha_init)
rfx_model$set_group_parameter_cov(sigma_xi_init)
rfx_model$set_variance_prior_shape(sigma_xi_shape)
rfx_model$set_variance_prior_scale(sigma_xi_scale)

# Random effect samples
rfx_samples <- createRandomEffectSamples(num_components, num_groups, rfx_tracker)

Prepare to run the sampler

num_warmstart <- 10
num_mcmc <- 100
num_samples <- num_warmstart + num_mcmc
global_var_samples <- c(global_variance_init, rep(0, num_samples))
leaf_scale_samples <- c(tau_init, rep(0, num_samples))

Run the grow-from-root sampler to “warm-start” BART

for (i in 1:num_warmstart) {
    # Sample forest
    forest_model$sample_one_iteration(
        forest_dataset, outcome, forest_samples, rng, feature_types, 
        outcome_model_type, leaf_prior_scale, var_weights, 
        global_var_samples[i], cutpoint_grid_size, gfr = T
    )
    
    # Sample global variance parameter
    global_var_samples[i+1] <- sample_sigma2_one_iteration(
        outcome, rng, nu, lambda
    )
    
    # Sample leaf node variance parameter and update `leaf_prior_scale`
    leaf_scale_samples[i+1] <- sample_tau_one_iteration(
        forest_samples, rng, a_leaf, b_leaf, i-1
    )
    leaf_prior_scale[1,1] <- leaf_scale_samples[i+1]
    
    # Sample random effects model
    rfx_model$sample_random_effect(rfx_dataset, outcome, rfx_tracker, rfx_samples, global_var_samples[i+1], rng)
}

Pick up from the last GFR forest (and associated global variance / leaf scale parameters) with an MCMC sampler

for (i in (num_warmstart+1):num_samples) {
    # Sample forest
    forest_model$sample_one_iteration(
        forest_dataset, outcome, forest_samples, rng, feature_types, 
        outcome_model_type, leaf_prior_scale, var_weights, 
        global_var_samples[i], cutpoint_grid_size, gfr = F
    )
    
    # Sample global variance parameter
    global_var_samples[i+1] <- sample_sigma2_one_iteration(
        outcome, rng, nu, lambda
    )
    
    # Sample leaf node variance parameter and update `leaf_prior_scale`
    leaf_scale_samples[i+1] <- sample_tau_one_iteration(
        forest_samples, rng, a_leaf, b_leaf, i-1
    )
    leaf_prior_scale[1,1] <- leaf_scale_samples[i+1]
    
    # Sample random effects model
    rfx_model$sample_random_effect(rfx_dataset, outcome, rfx_tracker, rfx_samples, global_var_samples[i+1], rng)
}

Predict and rescale samples

# Forest predictions
forest_preds <- forest_samples$predict(forest_dataset)*y_std + y_bar

# Random effects predictions
rfx_preds <- rfx_samples$predict(group_ids, rfx_basis)*y_std

# Overall predictions
preds <- forest_preds + rfx_preds

# Global error variance
sigma_samples <- sqrt(global_var_samples)*y_std

Results

Inspect the initial samples obtained via grow-from-root and an additive random effects model

plot(sigma_samples[1:num_warmstart], ylab="sigma")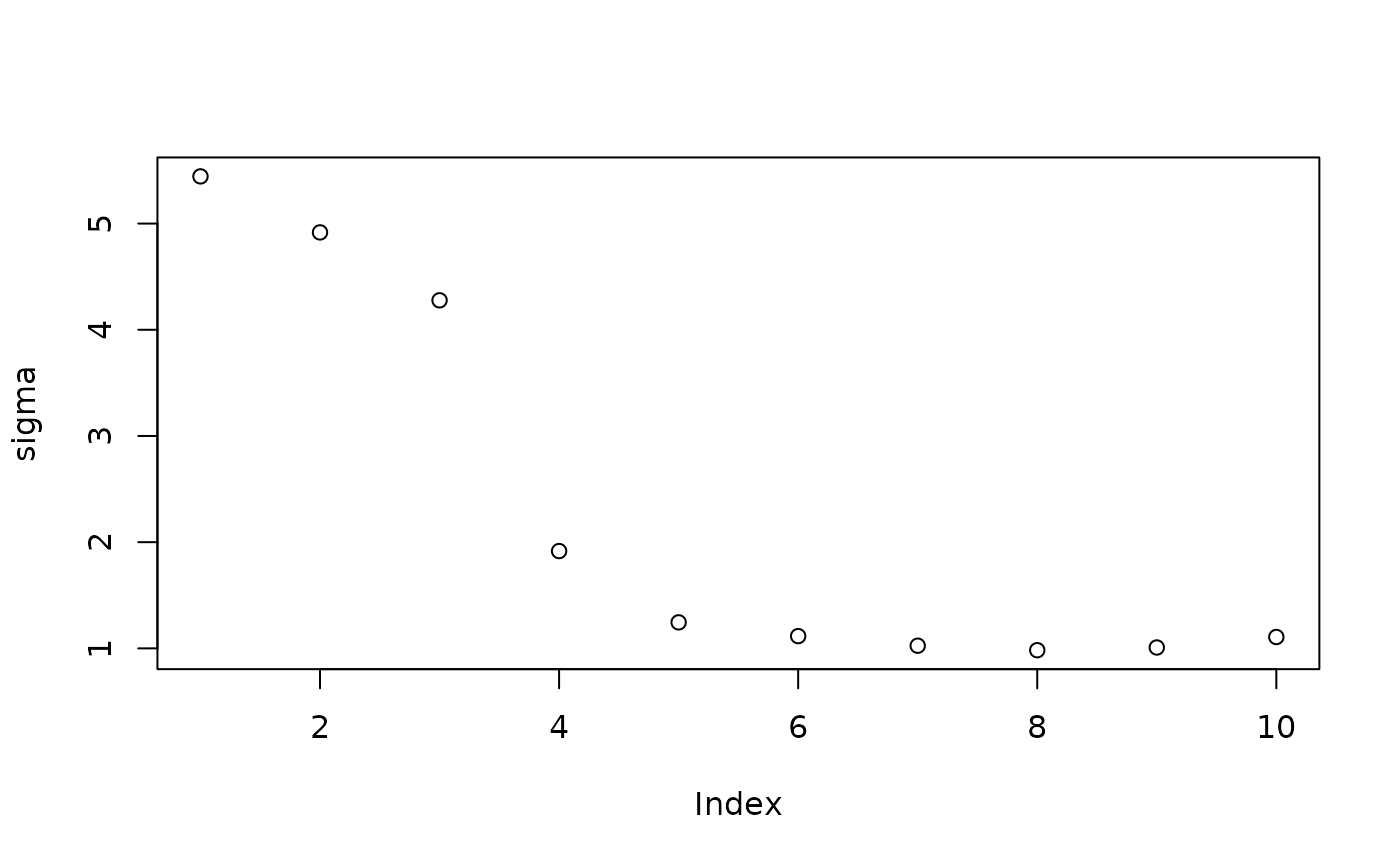

plot(rowMeans(preds[,1:num_warmstart]), y, pch=16, 
     cex=0.75, xlab = "pred", ylab = "actual")
abline(0,1,col="red",lty=2,lwd=2.5)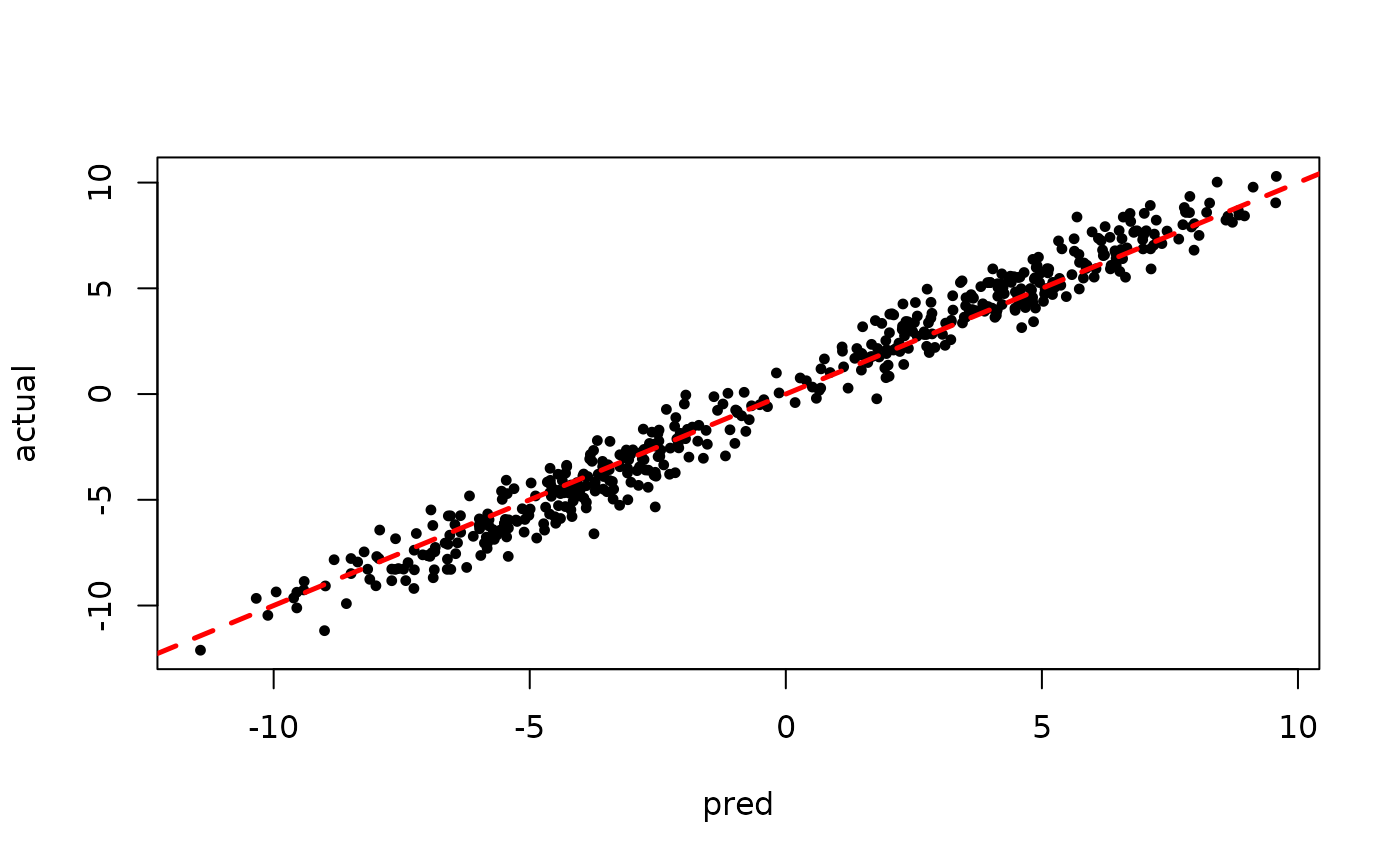

Inspect the BART samples obtained after “warm-starting” plus an additive random effects model

plot(sigma_samples[(num_warmstart+1):num_samples], ylab="sigma")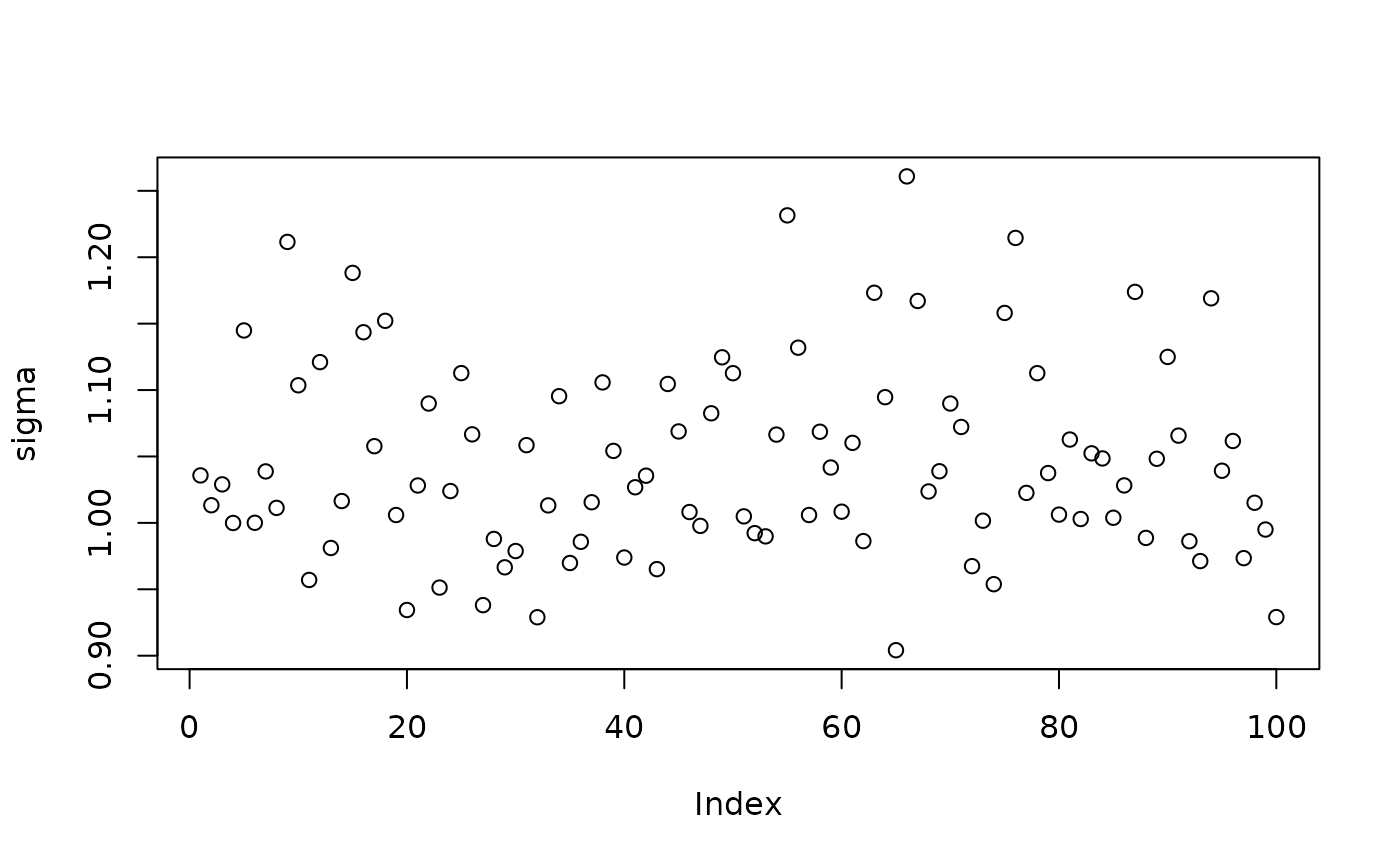

plot(rowMeans(preds[,(num_warmstart+1):num_samples]), y, pch=16, 
     cex=0.75, xlab = "pred", ylab = "actual")
abline(0,1,col="red",lty=2,lwd=2.5)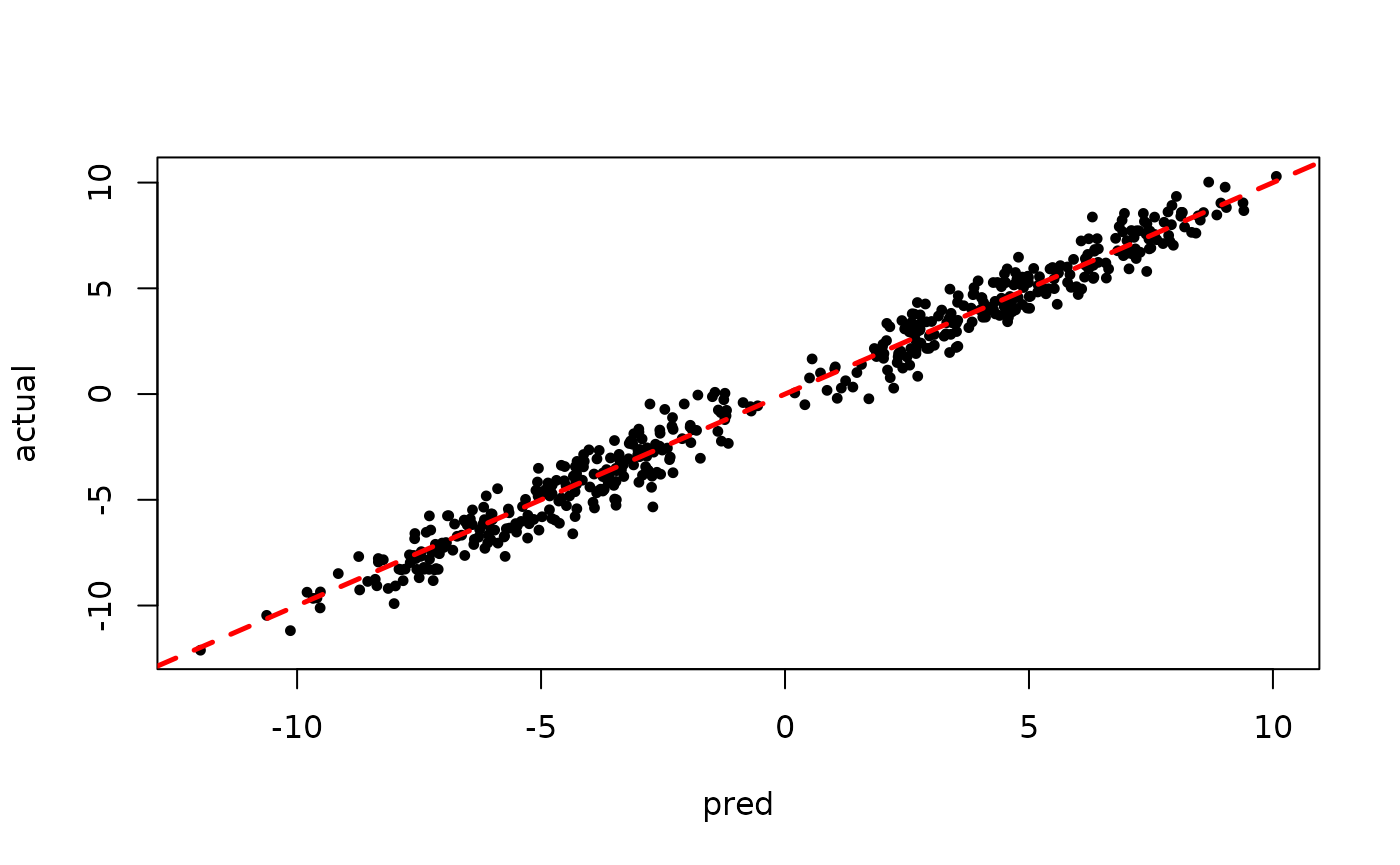

Now inspect the samples from the BART forest alone (without considering the random effect predictions)

plot(rowMeans(forest_preds[,(num_warmstart+1):num_samples]), y, pch=16, 
     cex=0.75, xlab = "pred", ylab = "actual")
abline(0,1,col="red",lty=2,lwd=2.5)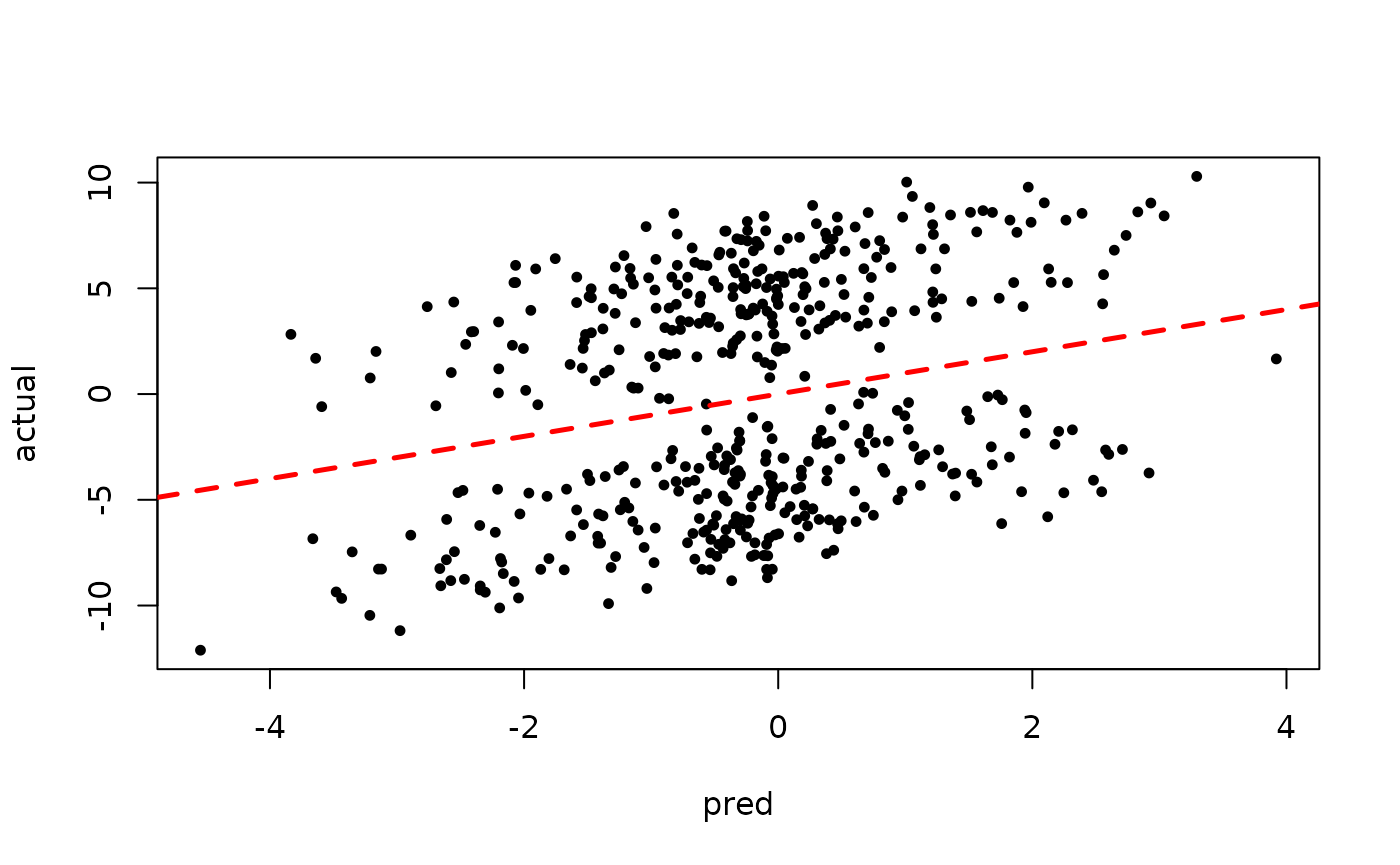

Demo 4: Causal Inference

Here we show how to implement the Bayesian Causal Forest (BCF) model of Hahn, Murray, and Carvalho (2020) using stochtree’s prototype API, including demoing a non-trivial sampling step done at the R level.

Background

While the supervised learning case of the previous demo is conceptually simple, we motivate the causal effect estimation task with some additional notation. Let \(y\) refer to a continuous outcome of interest, \(Z\) refer to a binary treatment, and \(X\) to a set of covariates that may influence \(Y\), \(Z\), or both.

If \(X\) is an exhaustive set of covariates that influence \(Z\) and \(Y\), we can specific \(Y\) in terms of a causal model (see for example Pearl (2009)) as \[\begin{equation*} \begin{aligned} Y &= F(Z, X, \epsilon_Y) \end{aligned} \end{equation*}\] where \(\epsilon_Y\) is outcome specific random noise and \(F\) is a function that generates \(Y\) (in many cases, \(F\) can be thought of as the inverse of the CDF conditional on \(X\) and \(Z\)).

The “potential outcomes” (see Imbens and Rubin (2015)) can be recovered by \(Y^1 = F(1, X, \epsilon_Y)\) and \(Y^0 = F(0, X, \epsilon_Y)\).

The causal outcome model can be decomposed into “mean” and “error” terms as below \[\begin{equation*} \begin{aligned} Y &= \mu(X) + Z\tau(X) + \left[\eta(X) + Z\delta(X)\right]\\ \mu(X) &= \mathbb{E}_{\epsilon_Y}\left[F(0, X, \epsilon_Y)\right]\\ \tau(X) &= \mathbb{E}_{\epsilon_Y}\left[F(1, X, \epsilon_Y) - F(0, X, \epsilon_Y)\right]\\ \eta(X) &= F(0, X, \epsilon_Y) - \mathbb{E}_{\epsilon_Y}\left[F(0, X, \epsilon_Y)\right]\\ \delta(X) &= F(1, X, \epsilon_Y) - F(0, X, \epsilon_Y) - \mathbb{E}_{\epsilon_Y}\left[F(1, X, \epsilon_Y) - F(0, X, \epsilon_Y)\right] \end{aligned} \end{equation*}\]

Here \(\tau(X)\) is precisely the conditional average treatment effect (CATE) estimand. Unfortunately, the functional form of \(F\) is unavailable for analysis, so that \(\tau(X)\) cannot be derived.

This is where flexible, regularized nonparametrics enter the picture, as we aim to estimate \(\mu(X)\) and \(\tau(X)\) from data.

Bayesian Causal Forest (BCF)

BCF estimates \(\mu(X)\) and \(\tau(X)\) using separate BART forests for each term. Furthermore, rather than rely on the common implicit coding of \(Z\) as 0 for control observations and 1 for treated observations, they consider coding control observations with a parameter \(b_0\) and treated observations with a parameter \(b_1\). Placing a \(N(0,1/2)\) prior on each \(b_z\), this essentially redefines the outcome model as \[\begin{equation*} \begin{aligned} y &= \mu(X) + \tau(X) f(Z) + \epsilon\\ f(Z) &= b_0(1-Z) + b_1 Z\\ \epsilon &\sim N\left(0, \sigma^2\right)\\ b_0, b_1 &\sim N\left(0, 1/2\right) \end{aligned} \end{equation*}\]

Updating each \(b_z\) requires an additional Gibbs step, which we derive here. Conditioning on sampled forests \(\mu\) and \(\tau\), we are essentially regressing \(y - \mu(Z)\) on \(\left[(1-Z)\tau(X), Z\tau(X)\right]\) which has a closed form posterior \[\begin{equation*} \begin{aligned} b_0 \mid y, X, \mu,\tau &\sim N\left(\frac{s_{y\tau,0}}{s_{\tau\tau,0} + 2\sigma^2}, \frac{\sigma^2}{s_{\tau\tau,0} + 2\sigma^2}\right)\\ b_1 \mid y, X, \mu,\tau &\sim N\left(\frac{s_{y\tau,1}}{s_{\tau\tau,1} + 2\sigma^2}, \frac{\sigma^2}{s_{\tau\tau,1} + 2\sigma^2}\right) \end{aligned} \end{equation*}\] where \(s_{y\tau,z} = \sum_{i: Z_i = z} (y_i - \mu(X_i))\tau(X_i)\) and \(s_{\tau\tau,z} = \sum_{i: Z_i = z} \tau(X_i)\tau(X_i)\).

Simulation

The simulated causal DGP mirrors the nonlinear, heterogeneous treatment effect DGP presented in Hahn, Murray, and Carvalho (2020).

n <- 500
x1 <- rnorm(n)
x2 <- rnorm(n)
x3 <- rnorm(n)
x4 <- as.numeric(rbinom(n,1,0.5))
x5 <- as.numeric(sample(1:3,n,replace=T))
X <- cbind(x1,x2,x3,x4,x5)
p <- ncol(X)
g <- function(x) {ifelse(x[,5]==1,2,ifelse(x[,5]==2,-1,4))}
mu1 <- function(x) {1+g(x)+x[,1]*x[,3]}
mu2 <- function(x) {1+g(x)+6*abs(x[,3]-1)}
tau1 <- function(x) {rep(3,nrow(x))}
tau2 <- function(x) {1+2*x[,2]*x[,4]}
mu_x <- mu1(X)
tau_x <- tau2(X)
pi_x <- 0.8*pnorm((3*mu_x/sd(mu_x)) - 0.5*X[,1]) + 0.05 + runif(n)/10
Z <- rbinom(n,1,pi_x)
E_XZ <- mu_x + Z*tau_x
snr <- 4
y <- E_XZ + rnorm(n, 0, 1)*(sd(E_XZ)/snr)

# Standardize outcome
y_bar <- mean(y)
y_std <- sd(y)
resid <- (y-y_bar)/y_std

Sampling

Set some parameters that inform the forest and variance parameter samplers

# Mu forest
alpha_mu <- 0.95
beta_mu <- 2.0
min_samples_leaf_mu <- 5
num_trees_mu <- 250
cutpoint_grid_size_mu = 100
tau_init_mu = 1/num_trees_mu
leaf_prior_scale_mu = matrix(c(tau_init_mu), ncol = 1)
a_leaf_mu <- 3.
b_leaf_mu <- var(resid)/(num_trees_mu)
leaf_regression_mu <- F
sigma_leaf_mu <- var(resid)/(num_trees_mu)
current_leaf_scale_mu <- as.matrix(sigma_leaf_mu)

# Tau forest
alpha_tau <- 0.25
beta_tau <- 3.0
min_samples_leaf_tau <- 5
num_trees_tau <- 50
cutpoint_grid_size_tau = 100
a_leaf_tau <- 3.
b_leaf_tau <- var(resid)/(2*num_trees_tau)
leaf_regression_tau <- T
sigma_leaf_tau <- var(resid)/(2*num_trees_tau)
current_leaf_scale_tau <- as.matrix(sigma_leaf_tau)

# Common parameters
nu <- 3
sigma2hat <- (sigma(lm(resid~X)))^2
quantile_cutoff <- 0.9
if (is.null(lambda)) {
    lambda <- (sigma2hat*qgamma(1-quantile_cutoff,nu))/nu
}
sigma2 <- sigma2hat
current_sigma2 <- sigma2

Prepare to run the sampler (now we must specify initial values for \(b_0\) and \(b_1\), for which we choose -1/2 and 1/2 instead of 0 and 1).

# Sampling composition
num_gfr <- 20
num_burnin <- 0
num_mcmc <- 100
num_samples <- num_gfr + num_burnin + num_mcmc

# Sigma^2 samples
global_var_samples <- rep(0, num_samples)

# Adaptive coding parameter samples
b_0_samples <- rep(0, num_samples)
b_1_samples <- rep(0, num_samples)
b_0 <- -0.5
b_1 <- 0.5
current_b_0 <- b_0
current_b_1 <- b_1
tau_basis <- (1-Z)*current_b_0 + Z*current_b_1

Initialize R-level access to the C++ classes needed to sample our model

# Data
X_mu <- cbind(X, pi_x)
X_tau <- X
feature_types <- c(0,0,0,1,1)
feature_types_mu <- as.integer(c(feature_types,0))
feature_types_tau <- as.integer(feature_types)
variable_weights_mu = rep(1/ncol(X_mu), ncol(X_mu))
variable_weights_tau = rep(1/ncol(X_tau), ncol(X_tau))
forest_dataset_mu <- createForestDataset(X_mu)
forest_dataset_tau <- createForestDataset(X_tau, tau_basis)
outcome <- createOutcome(resid)

# Random number generator (std::mt19937)
rng <- createRNG()

# Sampling data structures
forest_model_mu <- createForestModel(
    forest_dataset_mu, feature_types_mu, num_trees_mu, nrow(X_mu), 
    alpha_mu, beta_mu, min_samples_leaf_mu
)
forest_model_tau <- createForestModel(
    forest_dataset_tau, feature_types_tau, num_trees_tau, nrow(X_tau), 
    alpha_tau, beta_tau, min_samples_leaf_tau
)

# Container of forest samples
forest_samples_mu <- createForestContainer(num_trees_mu, 1, T)
forest_samples_tau <- createForestContainer(num_trees_tau, 1, F)

# Initialize the leaves of each tree in the prognostic forest
forest_samples_mu$set_root_leaves(0, mean(resid) / num_trees_mu)
forest_samples_mu$update_residual(
    forest_dataset_mu, outcome, forest_model_mu, F, 0, F
)

# Initialize the leaves of each tree in the treatment effect forest
forest_samples_tau$set_root_leaves(0, 0.)
forest_samples_tau$update_residual(
    forest_dataset_tau, outcome, forest_model_tau, T, 0, F
)

Run the grow-from-root sampler to “warm-start” BART, also updating the adaptive coding parameter \(b_0\) and \(b_1\)

if (num_gfr > 0){
    for (i in 1:num_gfr) {
        # Sample the prognostic forest
        forest_model_mu$sample_one_iteration(
            forest_dataset_mu, outcome, forest_samples_mu, rng, 
            feature_types_mu, 0, current_leaf_scale_mu, variable_weights_mu, 
            current_sigma2, cutpoint_grid_size, gfr = T, pre_initialized = T
        )
        
        # Sample variance parameters (if requested)
        global_var_samples[i] <- sample_sigma2_one_iteration(
            outcome, rng, nu, lambda
        )
        current_sigma2 <- global_var_samples[i]

        # Sample the treatment forest
        forest_model_tau$sample_one_iteration(
            forest_dataset_tau, outcome, forest_samples_tau, rng, 
            feature_types_tau, 1, current_leaf_scale_tau, variable_weights_tau, 
            current_sigma2, cutpoint_grid_size, gfr = T, pre_initialized = T
        )
        
        # Sample adaptive coding parameters
        mu_x_raw <- forest_samples_mu$predict_raw_single_forest(forest_dataset_mu, i-1)
        tau_x_raw <- forest_samples_tau$predict_raw_single_forest(forest_dataset_tau, i-1)
        s_tt0 <- sum(tau_x_raw*tau_x_raw*(Z==0))
        s_tt1 <- sum(tau_x_raw*tau_x_raw*(Z==1))
        partial_resid_mu <- resid - mu_x_raw
        s_ty0 <- sum(tau_x_raw*partial_resid_mu*(Z==0))
        s_ty1 <- sum(tau_x_raw*partial_resid_mu*(Z==1))
        current_b_0 <- rnorm(1, (s_ty0/(s_tt0 + 2*current_sigma2)), 
                             sqrt(current_sigma2/(s_tt0 + 2*current_sigma2)))
        current_b_1 <- rnorm(1, (s_ty1/(s_tt1 + 2*current_sigma2)), 
                             sqrt(current_sigma2/(s_tt1 + 2*current_sigma2)))
        tau_basis <- (1-Z)*current_b_0 + Z*current_b_1
        forest_dataset_tau$update_basis(tau_basis)
        b_0_samples[i] <- current_b_0
        b_1_samples[i] <- current_b_1
        
        # Sample variance parameters (if requested)
        global_var_samples[i] <- sample_sigma2_one_iteration(outcome, rng, nu, lambda)
        current_sigma2 <- global_var_samples[i]
    }
}

Pick up from the last GFR forest (and associated global variance / leaf scale parameters) with an MCMC sampler

if (num_burnin + num_mcmc > 0) {
    for (i in (num_gfr+1):num_samples) {
        # Sample the prognostic forest
        forest_model_mu$sample_one_iteration(
            forest_dataset_mu, outcome, forest_samples_mu, rng, feature_types_mu, 
            0, current_leaf_scale_mu, variable_weights_mu, current_sigma2, 
            cutpoint_grid_size, gfr = F, pre_initialized = T
        )
        
        # Sample global variance parameter
        global_var_samples[i] <- sample_sigma2_one_iteration(outcome, rng, nu, lambda)
        current_sigma2 <- global_var_samples[i]

        # Sample the treatment forest
        forest_model_tau$sample_one_iteration(
            forest_dataset_tau, outcome, forest_samples_tau, rng, feature_types_tau, 
            1, current_leaf_scale_tau, variable_weights_tau, current_sigma2, 
            cutpoint_grid_size, gfr = F, pre_initialized = T
        )
        
        # Sample coding parameters
        mu_x_raw <- forest_samples_mu$predict_raw_single_forest(forest_dataset_mu, i-1)
        tau_x_raw <- forest_samples_tau$predict_raw_single_forest(forest_dataset_tau, i-1)
        s_tt0 <- sum(tau_x_raw*tau_x_raw*(Z==0))
        s_tt1 <- sum(tau_x_raw*tau_x_raw*(Z==1))
        partial_resid_mu <- resid - mu_x_raw
        s_ty0 <- sum(tau_x_raw*partial_resid_mu*(Z==0))
        s_ty1 <- sum(tau_x_raw*partial_resid_mu*(Z==1))
        current_b_0 <- rnorm(1, (s_ty0/(s_tt0 + 2*current_sigma2)), 
                             sqrt(current_sigma2/(s_tt0 + 2*current_sigma2)))
        current_b_1 <- rnorm(1, (s_ty1/(s_tt1 + 2*current_sigma2)), 
                             sqrt(current_sigma2/(s_tt1 + 2*current_sigma2)))
        tau_basis <- (1-Z)*current_b_0 + Z*current_b_1
        forest_dataset_tau$update_basis(tau_basis)
        b_0_samples[i] <- current_b_0
        b_1_samples[i] <- current_b_1

        # Sample global variance parameter
        global_var_samples[i] <- sample_sigma2_one_iteration(outcome, rng, nu, lambda)
        current_sigma2 <- global_var_samples[i]
    }
}

Predict and rescale samples

# Forest predictions
mu_hat <- forest_samples_mu$predict(forest_dataset_mu)*y_std + y_bar
tau_hat_raw <- forest_samples_tau$predict_raw(forest_dataset_tau)
tau_hat <- t(t(tau_hat_raw) * (b_1_samples - b_0_samples))*y_std
y_hat <- mu_hat + tau_hat * as.numeric(Z)

# Global error variance
sigma2_samples <- global_var_samples*(y_std^2)

Results

Inspect the XBART results

plot(sigma2_samples[1:num_gfr], ylab="sigma^2")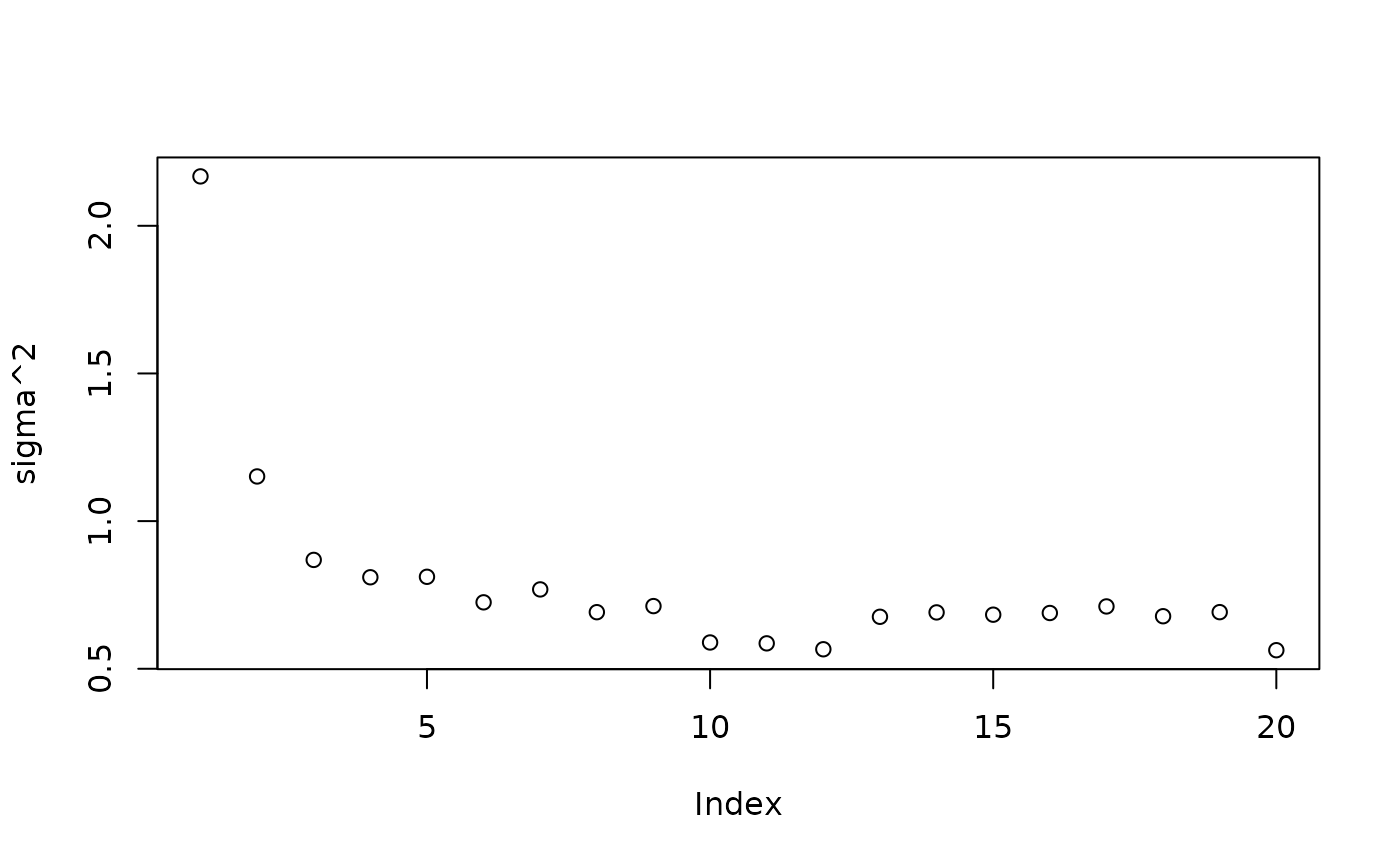

plot(rowMeans(mu_hat[,1:num_gfr]), mu_x, pch=16, cex=0.75, 
     xlab = "pred", ylab = "actual", main = "prognostic term")
abline(0,1,col="red",lty=2,lwd=2.5)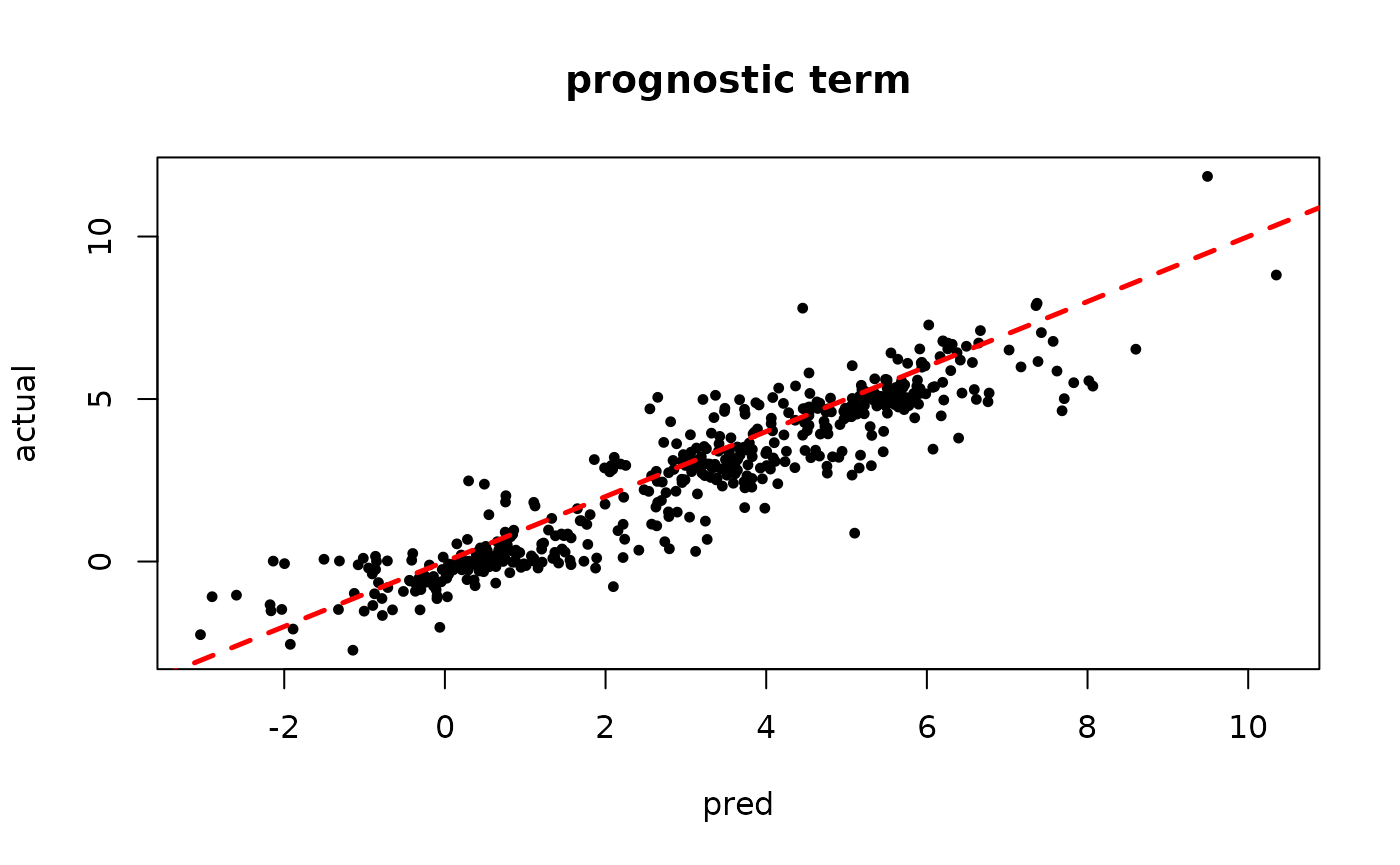

plot(rowMeans(tau_hat[,1:num_gfr]), tau_x, pch=16, cex=0.75, 
     xlab = "pred", ylab = "actual", main = "treatment effect term")
abline(0,1,col="red",lty=2,lwd=2.5)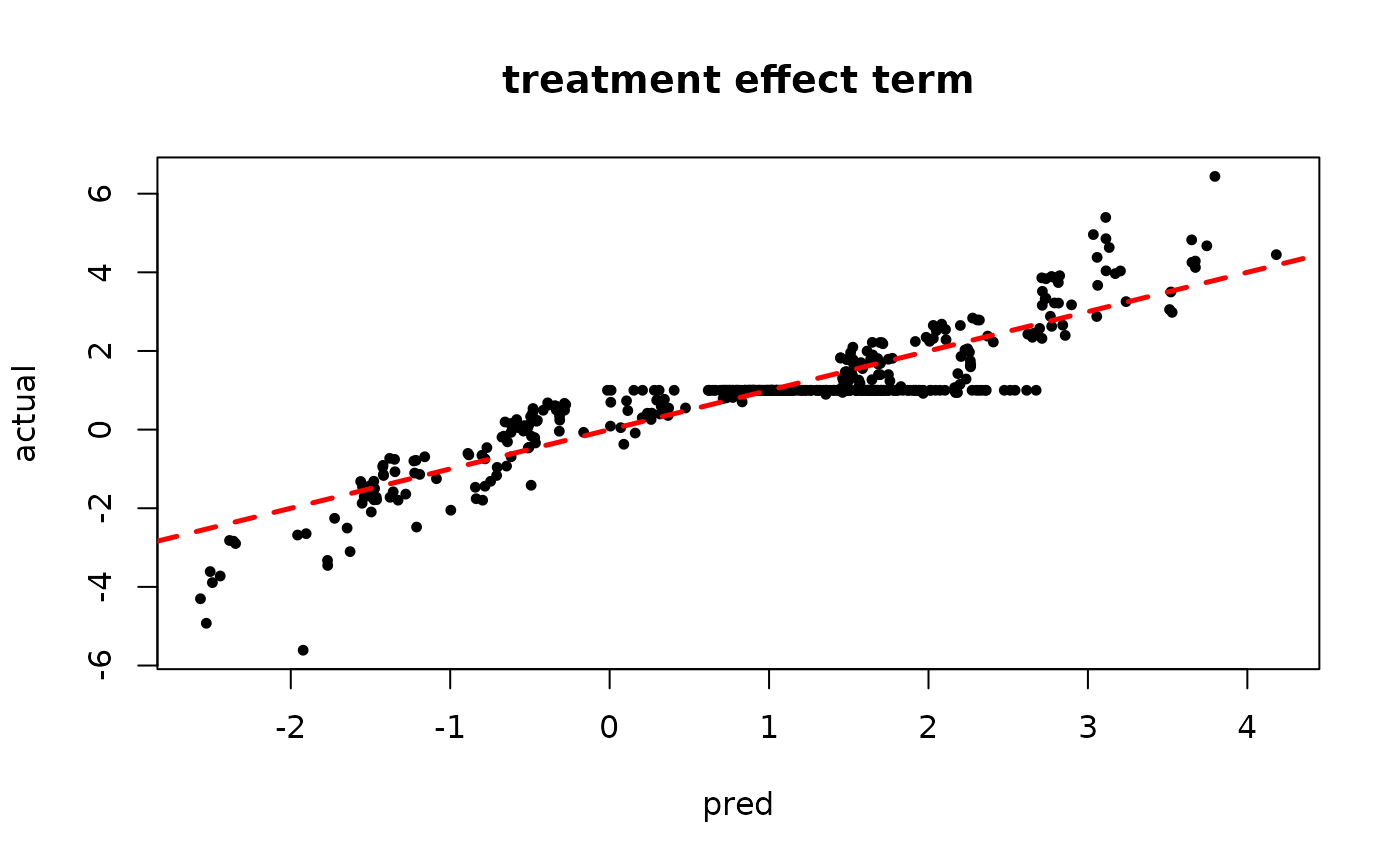

mean((rowMeans(tau_hat[,1:num_gfr]) - tau_x)^2)
#> [1] 0.4052996

Inspect the warm start BART results

plot(sigma_samples[(num_gfr+1):num_samples], ylab="sigma^2")

plot(rowMeans(mu_hat[,(num_gfr+1):num_samples]), mu_x, pch=16, cex=0.75, 
     xlab = "pred", ylab = "actual", main = "prognostic term")
abline(0,1,col="red",lty=2,lwd=2.5)

plot(rowMeans(tau_hat[,(num_gfr+1):num_samples]), tau_x, pch=16, cex=0.75, 
     xlab = "pred", ylab = "actual", main = "treatment effect term")
abline(0,1,col="red",lty=2,lwd=2.5)

mean((rowMeans(tau_hat[,(num_gfr+1):num_samples]) - tau_x)^2)
#> [1] 0.3371613

Inspect the “adaptive coding” parameters \(b_0\) and \(b_1\).

plot(b_0_samples, col = "blue", ylab = "Coding parameter draws", 
     ylim = c(min(min(b_0_samples), min(b_1_samples)), max(max(b_0_samples), max(b_1_samples))))
points(b_1_samples, col = "orange")
legend("topleft", legend = c("b_0", "b_1"), col = c("blue", "orange"), pch = c(1,1))

References

Hahn, P Richard, Jared S Murray, and Carlos M Carvalho. 2020. “Bayesian Regression Tree Models for Causal Inference: Regularization, Confounding, and Heterogeneous Effects (with Discussion).” Bayesian Analysis 15 (3): 965–1056.

He, Jingyu, and P Richard Hahn. 2023. “Stochastic Tree Ensembles for Regularized Nonlinear Regression.” Journal of the American Statistical Association 118 (541): 551–70.

Imbens, Guido W, and Donald B Rubin. 2015. Causal Inference in Statistics, Social, and Biomedical Sciences. Cambridge university press.

Murray, Jared S. 2021. “Log-Linear Bayesian Additive Regression Trees for Multinomial Logistic and Count Regression Models.” Journal of the American Statistical Association 116 (534): 756–69.

Pearl, Judea. 2009. Causality. Cambridge university press.

Pratola, Matthew T, Hugh A Chipman, Edward I George, and Robert E McCulloch. 2020. “Heteroscedastic BART via Multiplicative Regression Trees.” Journal of Computational and Graphical Statistics 29 (2): 405–17.